题目内容
8、关于直线与平面,有下列四个命题:
(1)若m∥α,n∥β,且α∥β,则m∥n;
(2)若m⊥α,n⊥β且α⊥β,则m⊥n;
(3)若m⊥α,n∥β且α∥β,则m⊥n;
(4)若m∥α,n⊥β且α⊥β,则m∥n;
其中不正确的命题为
(1)若m∥α,n∥β,且α∥β,则m∥n;
(2)若m⊥α,n⊥β且α⊥β,则m⊥n;
(3)若m⊥α,n∥β且α∥β,则m⊥n;
(4)若m∥α,n⊥β且α⊥β,则m∥n;
其中不正确的命题为
(1)(4)
.分析:根据面面平行的性质定理可判断(1),由线线、线面和面面垂直(平行)的定理判断(2)、(3)、(4).
解答:解:(1)根据面面平行的性质定理知,m和n是第三个平面与此平面的交线时,有m∥n,故(1)错误;
(2)∵α⊥β,m⊥α,∴在β存在与m平行的直线,再由n⊥β得m⊥n,故(2)正确;
(3)由m⊥α,α∥β得m⊥β,再由n∥β得m⊥n,故(3)正确;
(4)当m?β时,则m⊥n,故(4)错.
故答案为:(1)、(4).
(2)∵α⊥β,m⊥α,∴在β存在与m平行的直线,再由n⊥β得m⊥n,故(2)正确;
(3)由m⊥α,α∥β得m⊥β,再由n∥β得m⊥n,故(3)正确;
(4)当m?β时,则m⊥n,故(4)错.
故答案为:(1)、(4).
点评:本题考查了空间的线面位置关系,传统空间位置关系的判断依然是高考小题考查的重点,解决此类问题,注意定理中的关键条件以及特殊情况,主要根据垂直和平行定理进行判断,考查了空间想象能力.

练习册系列答案
相关题目
 中,把矩阵
中,把矩阵 确定的压缩变换
确定的压缩变换 与矩阵
与矩阵 确定的旋转变换
确定的旋转变换 进行复合,得到复合变换
进行复合,得到复合变换 .
.
 在复合变换
在复合变换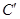 的方程.
的方程. 的参数方程为
的参数方程为 (
( 为参数),
为参数), 、
、 分别为直线
分别为直线 轴、
轴、 轴的交点,线段
轴的交点,线段 的中点为
的中点为 .
. 为极点,
为极点, 的极坐标方程.
的极坐标方程. 的解集与关于
的解集与关于 的解集相等.
的解集相等. ,
, 的值;
的值;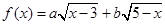 的最大值,以及取得最大值时
的最大值,以及取得最大值时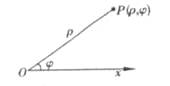 在平面上取定一点
在平面上取定一点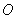 ,从
,从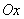 ,再取定一个长度单位及计算
,再取定一个长度单位及计算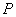 的位置就可以用线段
的位置就可以用线段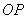
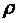 以及从
以及从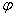 来确定,有序数对
来确定,有序数对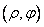 称为
称为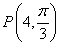 的极径为4,极角为
的极径为4,极角为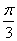 ;B.有序数对
;B.有序数对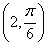 与
与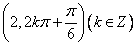 表示两个不同点;C.点
表示两个不同点;C.点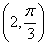 关于极点的对称点为
关于极点的对称点为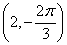 D.圆心在
D.圆心在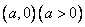 ,半径
,半径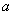 的圆的极坐标方程为
的圆的极坐标方程为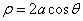 ;E.过点
;E.过点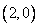 垂直极轴的直线方程为
垂直极轴的直线方程为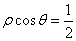 .其中真命题序号是
.
.其中真命题序号是
. 