题目内容
已知非零向量 、
、 满足
满足 ,若函数
,若函数
 在R上有极值,则
在R上有极值,则 的取值范围是( )
的取值范围是( )A.

B.

C.

D.

【答案】分析:根据三次函数在R上有极值,可知方程f′(x)=0有两个不等的实数根,从而判别式大于0,结合条件 ,可求
,可求 的取值范围.
的取值范围.
解答:解:∵

∴
令f′(x)=0
∵函数
 在R上有极值
在R上有极值
∴方程f′(x)=0有两个不等的实数根
∴
∵
∴
 >0
>0
∴
∵
∴
∴ 的取值范围是
的取值范围是
故选D.
点评:本题以函数极值为载体,考查导数知识的运用,考查向量的数量积,解题的关键是转化为方程f′(x)=0有两个不等的实数根.
 ,可求
,可求 的取值范围.
的取值范围.解答:解:∵


∴

令f′(x)=0
∵函数

 在R上有极值
在R上有极值∴方程f′(x)=0有两个不等的实数根
∴

∵

∴

 >0
>0∴

∵

∴

∴
 的取值范围是
的取值范围是
故选D.
点评:本题以函数极值为载体,考查导数知识的运用,考查向量的数量积,解题的关键是转化为方程f′(x)=0有两个不等的实数根.

练习册系列答案
相关题目
 )·
)·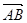 与
与 满足(
满足(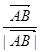 +
+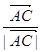 )·
)· =0,且
=0,且
 、
、 满足
满足 ,那么向量
,那么向量 与向量
与向量 的夹角为
的夹角为 B.
B. C.
C. D.
D.
 和
和 满足
满足 ,且
,且 ,
,