题目内容
已知抛物线y2=4x的焦点为F,准线为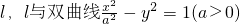 交于A,B两点,若△FAB为直角三角形,则双曲线的离心率是
交于A,B两点,若△FAB为直角三角形,则双曲线的离心率是
- A.

- B.

- C.2
- D.

B
分析:依题意,可求得物线的准线方程与焦点的坐标,从而可求得点A,B的坐标,利用 •
• =0可求得a2的值,从而可求得双曲线的离心率.
=0可求得a2的值,从而可求得双曲线的离心率.
解答:由抛物线y2=4x得:抛物线的准线方程为x=-1,抛物线的焦点F的坐标是(1,0).
令 -y2=1中的x=-1,得:
-y2=1中的x=-1,得: -y2=1,
-y2=1,
∴y2= -1
-1
∴y=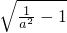 ,或y=-
,或y=-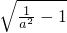 .
.
∴A、B的坐标分别是(-1,-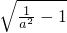 )、(-1,
)、(-1,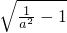 ).
).
∴向量 =(-2,-
=(-2,-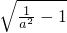 ),向量
),向量 =(-2,
=(-2,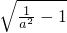 ).
).
∵△FAB是Rt△,显然有:| |=|
|=| |,
|, •
• =0,
=0,
∴4-( -1)=0
-1)=0
∴a2= ,
,
∴c2= +1=
+1= .
.
∴e2= =6,
=6,
∴e= .
.
∴双曲线的离心率是 .
.
故选B.
点评:本题考查双曲线与抛物线的简单性质,求得点A,B的坐标,利用 •
• =0求得a2的值是关键,也是难点,属于难题.
=0求得a2的值是关键,也是难点,属于难题.
分析:依题意,可求得物线的准线方程与焦点的坐标,从而可求得点A,B的坐标,利用
 •
• =0可求得a2的值,从而可求得双曲线的离心率.
=0可求得a2的值,从而可求得双曲线的离心率.解答:由抛物线y2=4x得:抛物线的准线方程为x=-1,抛物线的焦点F的坐标是(1,0).
令
 -y2=1中的x=-1,得:
-y2=1中的x=-1,得: -y2=1,
-y2=1,∴y2=
 -1
-1∴y=
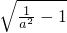 ,或y=-
,或y=-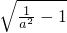 .
.∴A、B的坐标分别是(-1,-
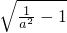 )、(-1,
)、(-1,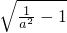 ).
).∴向量
 =(-2,-
=(-2,-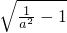 ),向量
),向量 =(-2,
=(-2,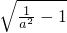 ).
).∵△FAB是Rt△,显然有:|
 |=|
|=| |,
|, •
• =0,
=0,∴4-(
 -1)=0
-1)=0∴a2=
 ,
,∴c2=
 +1=
+1= .
.∴e2=
 =6,
=6,∴e=
 .
.∴双曲线的离心率是
 .
.故选B.
点评:本题考查双曲线与抛物线的简单性质,求得点A,B的坐标,利用
 •
• =0求得a2的值是关键,也是难点,属于难题.
=0求得a2的值是关键,也是难点,属于难题. 
练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 已知抛物线y2=4x,焦点为F,顶点为O,点P(m,n)在抛物线上移动,Q是OP的中点,M是FQ的中点.
已知抛物线y2=4x,焦点为F,顶点为O,点P(m,n)在抛物线上移动,Q是OP的中点,M是FQ的中点.