题目内容
对于函数f（x）=
|x3|-
x2+（3-a）|x|+b，若f（x）有六个不同的单调区间，则a的取值范围为______．
| 1 |
| 3 |
| a |
| 2 |
∵函数f（x）=
|x3|-
x2+（3-a）|x|+b
∴f（-x）=f（x）
∴f（x）是偶函数
∵f（2）=7，
∴f（-2）=7
∵f（x）有六个不同的单调区间
又因为函数为偶函数
∴当x＞0时，有三个单调区间
即：f′（x）=x2-ax+3-a=0有两个不同的正根
∴
解得：2＜a＜3
故答案为：（2，3）
| 1 |
| 3 |
| a |
| 2 |
∴f（-x）=f（x）
∴f（x）是偶函数
∵f（2）=7，
∴f（-2）=7
∵f（x）有六个不同的单调区间
又因为函数为偶函数
∴当x＞0时，有三个单调区间
即：f′（x）=x2-ax+3-a=0有两个不同的正根
∴
|
解得：2＜a＜3
故答案为：（2，3）
练习册系列答案
相关题目
），有以下四个命题：①f（x）为奇函数；②f（x）的最小正周期为π，③f（x）在（0，
是f（x）的一条对称轴．其中真命题有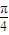
），有以下四个命题：①f（x）为奇函数；②f（x）的最小正周期为π，③f（x）在（0，
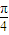）上单调递减，④x=
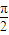是f（x）的一条对称轴．其中真命题有（ ）
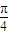），有以下四个命题：①f（x）为奇函数；②f（x）的最小正周期为π，③f（x）在（0，
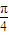）上单调递减，④x=
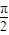是f（x）的一条对称轴．其中真命题有（ ）