Question

对于函数 f（x）与 g（x）和区间E，如果存在x∈E，使|f（x）-g（x）|＜1，则我们称函数 f（x）与 g（x）在区间E上“互相接近”．那么下列所给的两个函数在区间（0，+∞）上“互相接近”的是（ ）
A．f（x）=x²．g（x）=2x-3
B．（x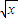）=，g（x）=x+2
C．f（x）=e^-x，g（x）=-
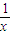
D．f（x）=lnx，g（x）=

Answer 1

【答案】分析：对照新定义，利用配方法、导数法可确定函数的值域，由此，就可以得出结论．
解答：解：对于A，f（x）-g（x）=x²-2x+3=（x-1）²+2≥2，∴不存在x∈（0，+∞），使|f（x）-g（x）|＜1，∴A不满足；
对于B，，∴不存在x∈（0，+∞），使|f（x）-g（x）|＜1，
∴B不满足；
对于C，h（x）=，h′（x）=＜0，∴函数在（0，+∞）上单调减，
∴x→0，h（x）→1，∴存在x∈（0，+∞），使|f（x）-g（x）|＜1，∴C满足；
对于D，h（x）=g（x）-f（x）=x-lnx（x＞0），h′（x）=，
令h′（x）＞0，可得x＞1，令h′（x）＜0，可得0＜x＜1，
∴x=1时，函数取得极小值，且为最小值，最小值为h（1）=1，∴g（x）-f（x）≥1，
∴不存在x∈（0，+∞），使|f（x）-g（x）|＜1，∴D不满足；
故选C．
点评：本题重点考查对新定义的理解与运用，考查配方法、导数法求函数的值域，有一定的综合性．