题目内容
已知函数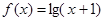 .
.
(Ⅰ)若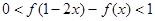 ,求
,求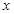 的取值范围;
的取值范围;
(Ⅱ)若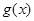 是以2为周期的偶函数,且当
是以2为周期的偶函数,且当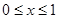 时,有
时,有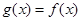 .
.
求当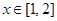 时,函数
时,函数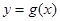 的解析式.
的解析式.
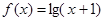 .
.(Ⅰ)若
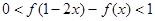 ,求
,求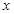 的取值范围;
的取值范围;(Ⅱ)若
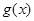 是以2为周期的偶函数,且当
是以2为周期的偶函数,且当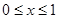 时,有
时,有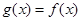 .
.求当
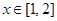 时,函数
时,函数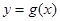 的解析式.
的解析式.(Ⅰ) 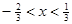 (Ⅱ)
(Ⅱ) 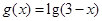
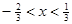 (Ⅱ)
(Ⅱ) 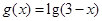
本试题主要是考查了函数解析式的求解和函数的单调性和奇偶性的综合运用以及不等式的求解问题。
(1)因为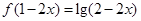
由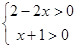 ,得
,得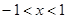 .
.
由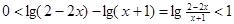 得
得 求解交集得到结论。
求解交集得到结论。
(2)因为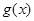 是以2为周期的偶函数,且当
是以2为周期的偶函数,且当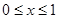 时,有
时,有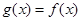
当xÎ2时,2-xÎ,因此
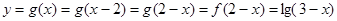 那么可知结论。
那么可知结论。
解:(Ⅰ)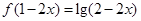
由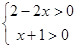 ,得
,得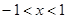 .
.
由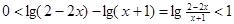 得
得
因为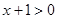 ,所以
,所以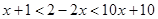 ,
,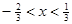 .
.
由 得
得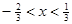
(Ⅱ)当xÎ2时,2-xÎ,因此
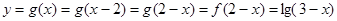
即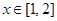 时,
时,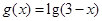
(1)因为
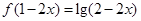
由
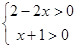 ,得
,得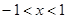 .
. 由
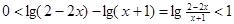 得
得 求解交集得到结论。
求解交集得到结论。(2)因为
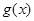 是以2为周期的偶函数,且当
是以2为周期的偶函数,且当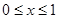 时,有
时,有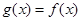
当xÎ2时,2-xÎ,因此
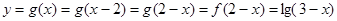 那么可知结论。
那么可知结论。解:(Ⅰ)
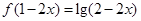
由
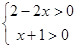 ,得
,得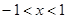 .
. 由
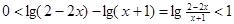 得
得
因为
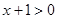 ,所以
,所以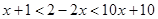 ,
,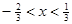 .
. 由
 得
得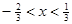
(Ⅱ)当xÎ2时,2-xÎ,因此
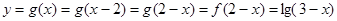
即
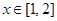 时,
时,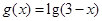

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案
相关题目
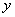 轴相交; ②定义在
轴相交; ②定义在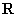 上的奇函数
上的奇函数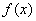 必满足
必满足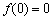 ;
;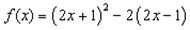 既不是奇函数又不是偶函数;
既不是奇函数又不是偶函数;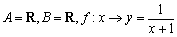 ,则
,则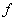 为
为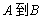 的映射;
的映射;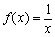 在
在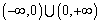 上是减函数.
上是减函数.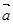 ="(1,2),"
="(1,2)," 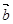 =(-2,1),k,t为正实数,向量
=(-2,1),k,t为正实数,向量  =
= 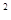 +1)
+1)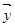 =-k
=-k
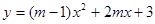 是偶函数,则
是偶函数,则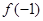 ,
, ,
,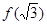 的大小关系为( )
的大小关系为( )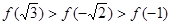
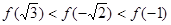
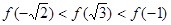
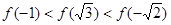
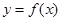 的周期为2,当
的周期为2,当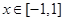 时
时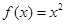 ,那么函数
,那么函数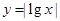 的图象的交点共有
的图象的交点共有 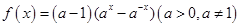 .
.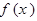 的奇偶性;
的奇偶性; 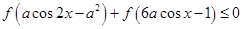 对任意
对任意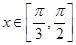 恒成立,求
恒成立,求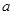 的取值范围.
的取值范围.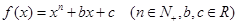
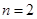 ,
,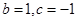 ,当
,当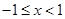 时,求
时,求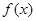 的单调区间和值域;
的单调区间和值域;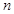 为偶数时,
为偶数时,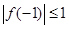 ,
,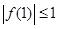 ,求
,求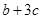 的最小值和最大值.
的最小值和最大值.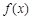 满足
满足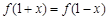 ,且
,且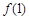 ,最小值是
,最小值是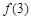
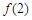
 =
=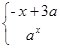
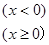
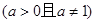 是R上的减函数,则
是R上的减函数,则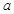 取值范围是( )
取值范围是( )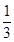 )
)