题目内容
2.已知tanα、tanβ为是于x的方程x2+px+q=0的两根,则sin2(α+β)+psin(α+β)cos(α+β)+qcos2(α+β)的值为q.分析 因为tanα,tanβ是方程x2+px+q=0的两根,所以根据根与系数的关系求出tanα+tanβ和tanαtanβ的值,然后利用两角和正切函数公式求出tan(α+β)的值,把所求的式子提取cos2(α+β)=$\frac{1}{1+ta{n}^{2}(α+β)}$后得到关于tan(α+β)的关系式,把tan(α+β)的值代入即可求出值.
解答 解:(1)由韦达达定理知$\left\{\begin{array}{l}{tanα+tanβ=-p}\\{tanα•tanβ=q}\end{array}\right.$,又tan(α+β)=$\frac{tanα+tanβ}{1-tanαtanβ}$=-$\frac{p}{1-q}$,
∴sin2(α+β)+psin(α+β)cos(α+β)+qcos2(α+β)
cos2(α+β)[tan2(α+β)+ptan(α+β)+q]
=$\frac{1}{1+ta{n}^{2}(α+β)}$[tan2(α+β)+ptan(α+β)+q]
=$\frac{1}{1+\frac{{p}^{2}}{(q-1)^{2}}}$[$\frac{{p}^{2}}{(q-1)^{2}}$+$\frac{{p}^{2}}{q-1}$+q]
=$\frac{q(1+{p}^{2}+{q}^{2}-2q)}{1+{p}^{2}+{q}^{2}-2q}$
=q.
故答案为:q.
点评 考查学生灵活运用两角和与差的正切函数公式及同角三角函数间的基本关系化简求值,灵活运用韦达定理解决数学问题,属于中档题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
 .
. 时,求函数
时,求函数 的最大值;
的最大值; 与
与 轴交于两点
轴交于两点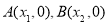 且
且 ,证明:
,证明: .
. 某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的体积为$\frac{80π}{3}$立方米,且l≥2r.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为c(c>5)千元.设该容器的建造费用为y千元.
某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的体积为$\frac{80π}{3}$立方米,且l≥2r.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为c(c>5)千元.设该容器的建造费用为y千元.