题目内容
已知圆C1的方程为 ,定直线l的方程为
,定直线l的方程为 .动圆C与圆C1外切,且与直线l相切.
.动圆C与圆C1外切,且与直线l相切.
(Ⅰ)求动圆圆心C的轨迹M的方程;
(2)直线 与轨迹M相切于第一象限的点P,过点P作直线
与轨迹M相切于第一象限的点P,过点P作直线 的垂线恰好经过点A(0,6),并交轨迹M于异于点P的点Q,记
的垂线恰好经过点A(0,6),并交轨迹M于异于点P的点Q,记 为
为 POQ(O为坐标原点)的面积,求
POQ(O为坐标原点)的面积,求 的值
的值

【答案】
Ⅰ)设动圆圆心C的坐标为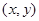 ,动圆半径为R,
,动圆半径为R,
则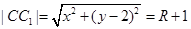 ,且
,且 ..........2分
..........2分
可得 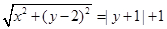 .............3分
.............3分
由于圆C1在直线l的上方,所以动圆C的圆心C应该在直线l的上方,所以有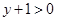 ,
,
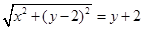 ,整理得
,整理得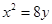 ,即为动圆圆心C的轨迹M的方程.....5分
,即为动圆圆心C的轨迹M的方程.....5分
(2)如图示,设点P的坐标为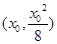 ,则
,则
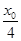 ,........6分
,........6分
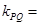
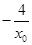 ,所以直线PQ的方程为
,所以直线PQ的方程为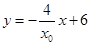 ........................8分
........................8分
又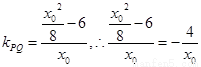 ,
,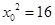 .
.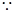 点P在第一象限,
点P在第一象限,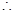
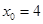 ,--9分
,--9分
点P坐标为(4,2),直线PQ的方程为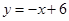 .--------------10分
.--------------10分
联立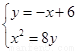 得
得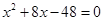 ,解得
,解得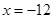 或4,
或4, 点Q的坐标为
点Q的坐标为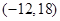 .所以
.所以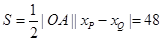
【解析】I)设动点C(x,y) ,然后根据条件建立方程,再化简即可,化简时要注意等价转化.不可增解和少解.
(II)解决此题的关键是先求出直线PQ的方程,可以设点P的坐标为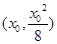 ,然后根据导数求出以P为切点的斜率,把切线方程表示出来,根据过点A,建立关于x0的方程,求出x0,问题得解.
,然后根据导数求出以P为切点的斜率,把切线方程表示出来,根据过点A,建立关于x0的方程,求出x0,问题得解.

练习册系列答案
相关题目
已知圆C1的方程为f(x,y)=0,且P(x0,y0)在圆C1外,圆C2的方程为f(x,y)=f(x0,y0),则C1与圆
C2一定( )
C2一定( )
| A、相离 | B、相切 | C、同心圆 | D、相交 |
 已知圆C1的方程为(x-4)2+(y-1)2=
已知圆C1的方程为(x-4)2+(y-1)2= 如图,已知圆C1的方程为
如图,已知圆C1的方程为