Question

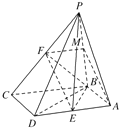
【题目】如图，四棱锥P－ABCD的底面ABCD是平行四边形，BA＝BD＝，AD＝2，PA＝PD＝，E，F分别是棱AD，PC的中点．

（1）证明：EF∥平面PAB；

（2）若二面角P－AD－B为60°．

①证明：平面PBC⊥平面ABCD；

②求直线EF与平面PBC所成角的正弦值．

Answer 1

【答案】（1）证明见解析；（2）①证明见解析；②．

【解析】

试题分析：（1）要证明平面，可以先证明平面，利用线面平行的判定定理，即可证明平面；（2）①要证明平面平面，可用面面垂直的判定定理，即只需证明平面即可；②由①平面，所以为直线与平面所成的角，由及已知，得为直角，即可计算的长度，在中，即计算直线与平面所成的角的正弦值．

试题解析：（1）证明：如图，取PB中点M，连接MF，AM．

因为F为PC中点，故MF∥BC且MF＝BC．由已知有BC∥AD，BC＝AD．

又由于E为AD中点，因而MF∥AE且MF＝AE，故四边形AMFE为平行四边形，

所以EF∥AM．又AM平面PAB，而EF平面PAB，所以EF∥平面PAB．

（2）①证明：如图，连接PE，BE．

因为PA＝PD，BA＝BD，而E为AD中点，故PE⊥AD，BE⊥AD，

所以∠PEB为二面角P－AD－B的平面角．

在△PAD中，由PA＝PD＝，AD＝2，可解得PE＝2．

在△ABD中，由BA＝BD＝，AD＝2，可解得BE＝1．

在△PEB中，PE＝2，BE＝1，∠PEB＝60°，由余弦定理，可解得PB＝，

从而∠PBE＝90°，即BE⊥PB．

又BC∥AD，BE⊥AD，从而BE⊥BC，因此BE⊥平面PBC．

又BE平面ABCD，所以平面PBC⊥平面ABCD．

②连接BF．由①知，BE⊥平面PBC，所以∠EFB为直线EF与平面PBC所成的角．

由PB＝及已知，得∠ABP为直角．

而MB＝PB＝，可得AM＝，故EF＝．

又BE＝1，故在Rt△EBF中，sin∠EFB＝＝．

所以直线EF与平面PBC所成角的正弦值为．