Question

【题目】平面直角坐标系 中，倾斜角为 的直线 过点 ，以原点 为极点， 轴的正半轴为极轴，建立极坐标系，曲线 的极坐标方程为 .
（1）写出直线 的参数方程( 为常数)和曲线 的直角坐标方程；
（2）若直线 与 交于 、 两点，且 ，求倾斜角 的值.

Answer 1

【答案】
（1）解：直线 的参数方程为 ( 为参数)，
曲线 的直角坐标方程：
（2）解：把直线的参数方程代入 ，得 ，
， ，
根据直线参数的几何意义， ，
得 或 .
又因为 ，
所以 .
【解析】（1）结合直角坐标系中直线的特征求得直线l的参数方程，求曲线C的直角坐标方程时先利用极坐标系将曲线C的方程化为参数方程，再求得其直角坐标方程；（2）利用交点的特征表示出点A，B坐标之间的关系，再根据直线参数的几何意义表示出两个模长的积，从而求得α的值，同时需根据点A，B的存在性判断α是否适合.
【考点精析】本题主要考查了极坐标系和直线的参数方程的相关知识点，需要掌握平面内取一个定点O，叫做极点；自极点O引一条射线OX叫做极轴；再选定一个长度单位、一个角度单位(通常取弧度)及其正方向(通常取逆时针方向)，这样就建立了一个极坐标系；经过点，倾斜角为的直线的参数方程可表示为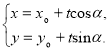（为参数）才能正确解答此题．