题目内容
(08年重庆一中一模理)(本小题满分13分,其中⑴小问4分,⑵小问4分,⑶小问5分)已知函数![]() 的导函数为
的导函数为![]() ,
,![]() 。⑴当
。⑴当![]() 时,求函数
时,求函数![]() 的单调区间;⑵若对满足
的单调区间;⑵若对满足![]() 的一切
的一切![]() 的值,都有
的值,都有![]() ,求实数
,求实数![]() 的取值范围;⑶若
的取值范围;⑶若![]() 对一切
对一切![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围。
的取值范围。
解析:⑴当![]() 时,
时,![]() 。令
。令![]() 得
得![]() ,故当
,故当![]() 时
时![]() ,
,![]() 单调递增;当
单调递增;当![]() 时
时![]() ,
,![]() 单调递减。所以函数
单调递减。所以函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;
;
⑵法一:因![]() ,故
,故![]() 。令
。令![]() ,要使
,要使![]() 对满足
对满足![]() 的一切
的一切![]() 成立,则
成立,则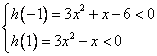 ,解得
,解得![]() ;
;
法二:![]() ,故
,故![]() 。由
。由![]() 可解得
可解得
![]() 。因为
。因为![]() 在
在![]() 单调
单调
递减,因此![]() 在
在![]() 单调递增,故
单调递增,故![]() 。设
。设


练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
相关题目
