题目内容
已知数列{an}满足 ,数列{bn}满足bn=lnan.
,数列{bn}满足bn=lnan.(1)求数列{an}的通项公式;
(2)试比较
 的大小,并说明理由.
的大小,并说明理由.
【答案】分析:(1)取倒数,可得{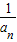 }是以
}是以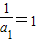 为首项,1为公差的等差数列,即可求得{
为首项,1为公差的等差数列,即可求得{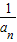 }的通项公式,从而可得数列{an}的通项公式.
}的通项公式,从而可得数列{an}的通项公式.
(2)构造函数f(x)=lnx-x+1,求导研究出f(x)的单调性,即可得到结论.
解答:解:(1)∵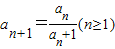 ,∴
,∴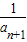 =
=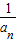 +1
+1
∴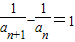
∴{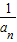 }是以
}是以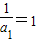 为首项,1为公差的等差数列
为首项,1为公差的等差数列
∴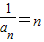 ,∴an=
,∴an=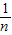 ;
;
(2)由(1)得an-1=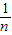 -1,bn=lnan=ln
-1,bn=lnan=ln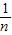
构造函数f(x)=lnx-x+1,则f′(x)=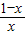
当0<x<1时,f'(x)>0,f(x)在(0,1)上单调递增;
当x>1时,f'(x)<0,f(x)在(1,+∞)上单调递减,
∴f(x)≤f(1)=0,
即?x>0,lnx≤x-1,当且仅当x=1时取等号,
∴ln ≤
≤ -1,即bi≤ai-1,当且仅当i=1时取等号,
-1,即bi≤ai-1,当且仅当i=1时取等号,
∴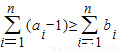 ,当且仅当i=1时取等号.
,当且仅当i=1时取等号.
点评:本题是函数与导数、数列、不等式的综合,考查学生分析解决问题的能力,属于中档题.
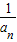 }是以
}是以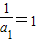 为首项,1为公差的等差数列,即可求得{
为首项,1为公差的等差数列,即可求得{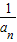 }的通项公式,从而可得数列{an}的通项公式.
}的通项公式,从而可得数列{an}的通项公式.(2)构造函数f(x)=lnx-x+1,求导研究出f(x)的单调性,即可得到结论.
解答:解:(1)∵
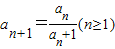 ,∴
,∴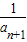 =
=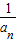 +1
+1∴
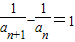
∴{
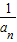 }是以
}是以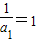 为首项,1为公差的等差数列
为首项,1为公差的等差数列∴
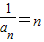 ,∴an=
,∴an=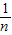 ;
;(2)由(1)得an-1=
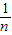 -1,bn=lnan=ln
-1,bn=lnan=ln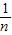
构造函数f(x)=lnx-x+1,则f′(x)=
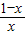
当0<x<1时,f'(x)>0,f(x)在(0,1)上单调递增;
当x>1时,f'(x)<0,f(x)在(1,+∞)上单调递减,
∴f(x)≤f(1)=0,
即?x>0,lnx≤x-1,当且仅当x=1时取等号,
∴ln
 ≤
≤ -1,即bi≤ai-1,当且仅当i=1时取等号,
-1,即bi≤ai-1,当且仅当i=1时取等号,∴
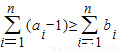 ,当且仅当i=1时取等号.
,当且仅当i=1时取等号.点评:本题是函数与导数、数列、不等式的综合,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目