题目内容
设函数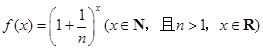
(Ⅰ)当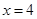 时,求
时,求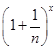 的展开式中二项式系数最大的项;
的展开式中二项式系数最大的项;
(Ⅱ)对任意的实数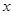 ,证明 :
,证明 :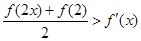 (
(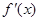 是
是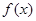 的导函数);
的导函数);
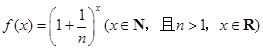
(Ⅰ)当
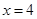 时,求
时,求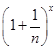 的展开式中二项式系数最大的项;
的展开式中二项式系数最大的项;(Ⅱ)对任意的实数
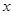 ,证明 :
,证明 :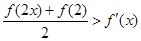 (
(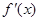 是
是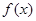 的导函数);
的导函数);(Ⅰ) (Ⅱ)见解析
(Ⅱ)见解析
 (Ⅱ)见解析
(Ⅱ)见解析本试题主要考查了二项式定理的运用,以及二项式系数的最大项的问题,和运用函数的思想解决不等式的恒成立问题的综合运用。
(1)中,根据二项式系数的性质可知,二项式系数的最大项取决于幂指数为奇数还是偶数来得到
(2)中利用均值不等式的思想,表示出
 和放缩法的思想得到
和放缩法的思想得到
(Ⅰ)解:展开式中二项式系数最大的项是第3项,这项是
(Ⅱ)证法一:因





证法二:
因


而
故只需对 和
和 进行比较。
进行比较。
令 ,有
,有 由
由 ,得
,得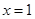
因为当 时,
时, ,
, 单调递减;当
单调递减;当 时,
时,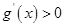 ,
, 单调递增,所以在
单调递增,所以在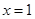 处
处 有极小值
有极小值 故当
故当 时,
时, ,
,
从而有 ,亦即
,亦即 故有
故有 恒成立。
恒成立。
所以 ,原不等式成立。
,原不等式成立。
(1)中,根据二项式系数的性质可知,二项式系数的最大项取决于幂指数为奇数还是偶数来得到
(2)中利用均值不等式的思想,表示出

 和放缩法的思想得到
和放缩法的思想得到(Ⅰ)解:展开式中二项式系数最大的项是第3项,这项是

(Ⅱ)证法一:因






证法二:
因



而

故只需对
 和
和 进行比较。
进行比较。令
 ,有
,有 由
由 ,得
,得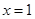
因为当
 时,
时, ,
, 单调递减;当
单调递减;当 时,
时,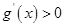 ,
, 单调递增,所以在
单调递增,所以在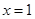 处
处 有极小值
有极小值 故当
故当 时,
时, ,
,从而有
 ,亦即
,亦即 故有
故有 恒成立。
恒成立。所以
 ,原不等式成立。
,原不等式成立。
练习册系列答案
相关题目
 与
与
 与
与
 与
与
 与
与

 时,求不等式
时,求不等式 的解集;
的解集; 的解集包含
的解集包含 ,求
,求 的取值范围.
的取值范围.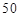 至
至 人之间,游客人数
人之间,游客人数 (人)与游客的消费总额
(人)与游客的消费总额 (元)之间近似地满足关系:
(元)之间近似地满足关系: .那么游客的人均消费额最高为_________元
.那么游客的人均消费额最高为_________元 是偶函数,则函数图像与
是偶函数,则函数图像与 轴交点的纵坐标的最大值是______.
轴交点的纵坐标的最大值是______. 的最大值和最小值分别为
的最大值和最小值分别为
 ,
,


 是定义在
是定义在 上的函数,其图象是一条连续的曲线,且满足下列条件:①
上的函数,其图象是一条连续的曲线,且满足下列条件:① ,
, ∈
∈ |<|
|<| 立方米时,只付基本费9元和每户每月定额损耗费
立方米时,只付基本费9元和每户每月定额损耗费 元;
元; 元的超额费;
元的超额费; (元)与月用水量
(元)与月用水量 (立方米)的函数关系式;
(立方米)的函数关系式; 的值。
的值。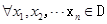 ,都有
,都有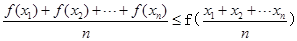 ,若
,若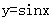 在区间
在区间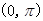 上是凸函数,那么在
上是凸函数,那么在 中,
中,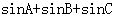 的最大值为( )
的最大值为( )


