题目内容
8.已知函数f(x)满足?x∈R,f(x)=f(2-x)且f(x)在区间[1,+∞)上单调递增,则满足$f(2x)<f(\frac{1}{3})$的x的取值范围是( )| A. | $(\frac{1}{5},\frac{5}{6})$ | B. | $[\frac{1}{5},\frac{5}{6})$ | C. | $(\frac{1}{6},\frac{5}{6})$ | D. | $[\frac{1}{6},\frac{5}{6})$ |
分析 由题意可知函数f(x)的图象关于直线x=1对称,再结合单调性可知|2x-1|<|$\frac{1}{3}$-1|,从而解得.
解答 解:∵f(x)=f(2-x),
∴函数f(x)的图象关于直线x=1对称,
∵f(x)在区间[1,+∞)上单调递增,
∴函数f(x)的图象开口向上,
∵$f(2x)<f(\frac{1}{3})$,
∴|2x-1|<|$\frac{1}{3}$-1|,
解得,$\frac{1}{6}$<x<$\frac{5}{6}$,
故选C.
点评 本题考查了函数的性质的判断与应用,同时考查了函数的单调性在解不等式时的应用.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
18.在三棱锥S-ABC中,SA⊥平面ABC,SA=4,底面△ABC是边长为3的正三角形,则三棱锥S-ABC的外接球的表面积为( )
| A. | 19π | B. | 28π | C. | 43π | D. | 76π |
19.下列说法正确的是( )
| A. | -1∈N | B. | $\sqrt{2}$∈Q | C. | π∉R | D. | ∅⊆Z |
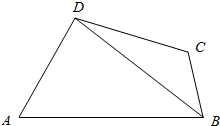 如图,在四边形ABCD中,AB=8,BC=3,CD=5,∠A=$\frac{π}{3}$,cos∠ADB=$\frac{1}{7}$.
如图,在四边形ABCD中,AB=8,BC=3,CD=5,∠A=$\frac{π}{3}$,cos∠ADB=$\frac{1}{7}$.