题目内容
已知函数f(x)=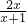 ,数列{an}满足a1=2,且an=
,数列{an}满足a1=2,且an= .
.
(1)求证:数列{ }是等差数列;
}是等差数列;
(2)对一切正整数n,令Sn=a1a2+a2a3+…+anan+1,求Sn.
解:(1)证明:由题意可得 an= ,∴
,∴ =1+
=1+ ,∴{
,∴{ }是以1为公差的等差数列.
}是以1为公差的等差数列.
(2)由(1)可得 =
= +(n-1)×1=
+(n-1)×1= ,∴an=
,∴an= .
.
故Sn=a1a2+a2a3+…+anan+1 =4× +4×
+4×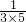 +4×
+4×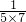 +…+4×
+…+4×
=4[1- +
+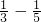 +
+ +…+
+…+ -
- ]=4×(1-
]=4×(1- )=
)= .
.
分析:(1)由题意可得 an= ,化简可得
,化简可得  =1+
=1+ ,从而得出结论.
,从而得出结论.
(2)由(1)可得 =
= +(n-1)×1=
+(n-1)×1= ,得 an=
,得 an= ,用裂项法求出Sn=a1a2+a2a3+…+anan+1 的值.
,用裂项法求出Sn=a1a2+a2a3+…+anan+1 的值.
点评:本题主要考查等差关系的确定,用裂项法对数列进行求和,属于中档题.
 ,∴
,∴ =1+
=1+ ,∴{
,∴{ }是以1为公差的等差数列.
}是以1为公差的等差数列.(2)由(1)可得
 =
= +(n-1)×1=
+(n-1)×1= ,∴an=
,∴an= .
.故Sn=a1a2+a2a3+…+anan+1 =4×
 +4×
+4×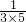 +4×
+4×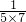 +…+4×
+…+4×
=4[1-
 +
+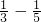 +
+ +…+
+…+ -
- ]=4×(1-
]=4×(1- )=
)= .
.分析:(1)由题意可得 an=
 ,化简可得
,化简可得  =1+
=1+ ,从而得出结论.
,从而得出结论.(2)由(1)可得
 =
= +(n-1)×1=
+(n-1)×1= ,得 an=
,得 an= ,用裂项法求出Sn=a1a2+a2a3+…+anan+1 的值.
,用裂项法求出Sn=a1a2+a2a3+…+anan+1 的值.点评:本题主要考查等差关系的确定,用裂项法对数列进行求和,属于中档题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|