Question

如图，从原点和A(5，2)为两个顶点作等腰直角三角形OAB，使∠B=90°，求点B和向量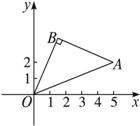的坐标.

Answer 1

思路分析：关键是求出B点的坐标，设B(x，y)，由⊥和||=||，则可列出x、y的方程组，解方程组，则可求得x、y，再求的坐标.

解：设B点坐标为(x，y)，则=(x，y)，=(x－5，y－2).

∵⊥，∴x(x－5)+y(y－2)=0,

即x²+y²－5x－2y=0.                                                      ①

又|OB|=|AB|，

∴x²+y²=(x－5)²+(y－2)²，

即10x+4y=29.                                                               ②

解①②,得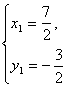或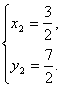

∴B点坐标为(，)或(，).

∴=(，)或=(，).

方法归纳 本题是构造方程的题目，主要是用两个向量垂直的充要条件,向量的减法、向量的模的定义，紧紧抓住“等腰”“直角”两个条件，把方程组列出来，在解方程组求解时,应注意代入消元思想的运用.