题目内容
已知二次函数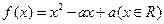 同时满足:①不等式
同时满足:①不等式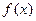 ≤0的解集有且只有一个元素;②在定义域内存在
≤0的解集有且只有一个元素;②在定义域内存在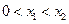 ,使得不等式
,使得不等式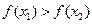 成立,设数列{
成立,设数列{ }的前
}的前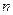 项和
项和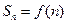 .
.
(1)求函数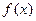 的表达式;
的表达式;
(2) 设各项均不为0的数列{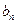 }中,所有满足
}中,所有满足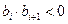 的整数
的整数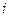 的个数称为这个数列{
的个数称为这个数列{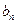 }的变号数,令
}的变号数,令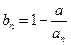 (
(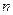
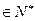 ),求数列{
),求数列{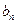 }的变号数;
}的变号数;
(3)设数列{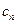 }满足:
}满足: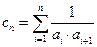 ,试探究数列{
,试探究数列{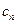 }是否存在最小项?若存在,求出该项,若不存在,说明理由.
}是否存在最小项?若存在,求出该项,若不存在,说明理由.
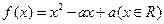 同时满足:①不等式
同时满足:①不等式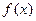 ≤0的解集有且只有一个元素;②在定义域内存在
≤0的解集有且只有一个元素;②在定义域内存在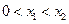 ,使得不等式
,使得不等式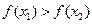 成立,设数列{
成立,设数列{ }的前
}的前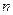 项和
项和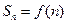 .
.(1)求函数
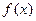 的表达式;
的表达式;(2) 设各项均不为0的数列{
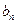 }中,所有满足
}中,所有满足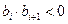 的整数
的整数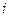 的个数称为这个数列{
的个数称为这个数列{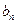 }的变号数,令
}的变号数,令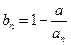 (
(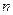
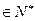 ),求数列{
),求数列{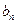 }的变号数;
}的变号数; (3)设数列{
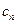 }满足:
}满足: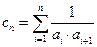 ,试探究数列{
,试探究数列{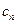 }是否存在最小项?若存在,求出该项,若不存在,说明理由.
}是否存在最小项?若存在,求出该项,若不存在,说明理由.(1) (2) 3
(2) 3
 (2) 3
(2) 3(1)∵不等式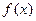 ≤0的解集有且只有一个元素
≤0的解集有且只有一个元素
∴ 解得
解得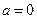 或
或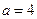 ----------2分
----------2分
当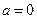 时函数
时函数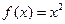 在
在 递增,不满足条件②
递增,不满足条件②
当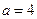 时函数
时函数 在(0,2)上递减,满足条件②
在(0,2)上递减,满足条件②
综上得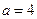 ,即
,即 ----------4分
----------4分
(2)由(1)知
当 时,
时,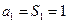 ,当
,当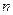 ≥2时
≥2时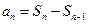 =
= =
=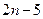
∴ -------6分由题设可得
-------6分由题设可得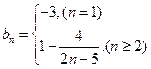 ----7分
----7分
∵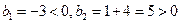 ,
,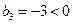 ,∴
,∴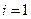 ,
,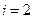 都满足
都满足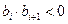
∵当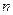 ≥3时,
≥3时,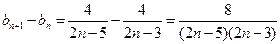
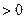
即当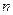 ≥3时,数列{
≥3时,数列{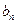 }递增,∵
}递增,∵
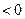 ,由
,由
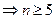 ,可知
,可知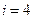 满足
满足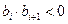 ∴数列{
∴数列{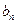 }的变号数为3。-----9分
}的变号数为3。-----9分
(3)∵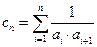 =
= , 由(2)可得:
, 由(2)可得:
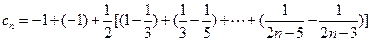 --------------11分
--------------11分
=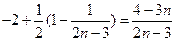 =
= -------13分
-------13分
∵当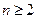 时数列{
时数列{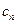 }递增,∴当
}递增,∴当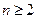 时,
时,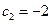 最小, 又∵
最小, 又∵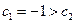 ,
,
∴数列{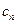 }存在最小项
}存在最小项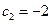 ------14分
------14分
〔或∵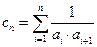 =
= ,由(2)可得:
,由(2)可得:
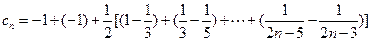 -----11分
-----11分
=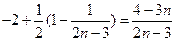
对于函数 ∵
∵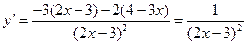
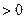
∴函数 在
在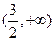 上为增函数,∴当
上为增函数,∴当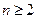 时数列{
时数列{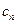 }递增,
}递增,
∴当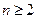 时,
时,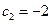 最小,---13分
最小,---13分
又∵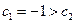 , ∴数列{
, ∴数列{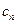 }存在最小项
}存在最小项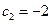 ---------14分〕
---------14分〕
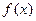 ≤0的解集有且只有一个元素
≤0的解集有且只有一个元素∴
 解得
解得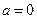 或
或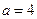 ----------2分
----------2分当
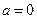 时函数
时函数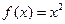 在
在 递增,不满足条件②
递增,不满足条件②当
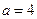 时函数
时函数 在(0,2)上递减,满足条件②
在(0,2)上递减,满足条件②综上得
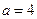 ,即
,即 ----------4分
----------4分(2)由(1)知

当
 时,
时,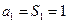 ,当
,当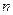 ≥2时
≥2时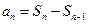 =
= =
=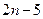
∴
 -------6分由题设可得
-------6分由题设可得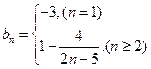 ----7分
----7分∵
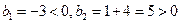 ,
,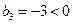 ,∴
,∴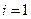 ,
,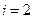 都满足
都满足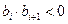
∵当
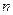 ≥3时,
≥3时,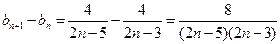
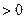
即当
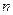 ≥3时,数列{
≥3时,数列{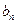 }递增,∵
}递增,∵
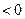 ,由
,由
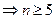 ,可知
,可知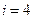 满足
满足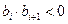 ∴数列{
∴数列{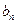 }的变号数为3。-----9分
}的变号数为3。-----9分(3)∵
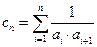 =
= , 由(2)可得:
, 由(2)可得: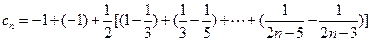 --------------11分
--------------11分=
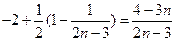 =
= -------13分
-------13分∵当
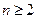 时数列{
时数列{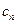 }递增,∴当
}递增,∴当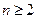 时,
时,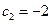 最小, 又∵
最小, 又∵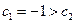 ,
,∴数列{
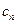 }存在最小项
}存在最小项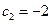 ------14分
------14分〔或∵
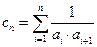 =
= ,由(2)可得:
,由(2)可得: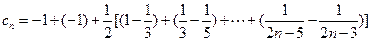 -----11分
-----11分=
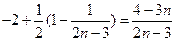
对于函数
 ∵
∵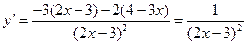
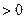
∴函数
 在
在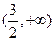 上为增函数,∴当
上为增函数,∴当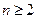 时数列{
时数列{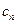 }递增,
}递增,∴当
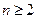 时,
时,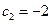 最小,---13分
最小,---13分又∵
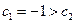 , ∴数列{
, ∴数列{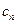 }存在最小项
}存在最小项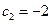 ---------14分〕
---------14分〕
练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
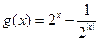 .
.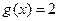 ,求
,求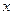 的值;
的值;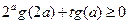 对于
对于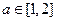 恒成立,求实数
恒成立,求实数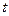 的取值范围.
的取值范围.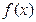 为奇函数,且在
为奇函数,且在 内是增函数,又
内是增函数,又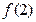
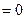 ,则
,则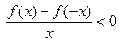 的解集为
的解集为

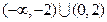
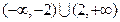
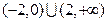
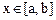 ,总有
,总有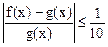 ,则称f(x)可被g(x)替代,试判断函数
,则称f(x)可被g(x)替代,试判断函数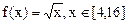 能否被
能否被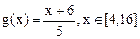 替代,并说明理由.
替代,并说明理由.

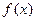 的定义域为R,若存在常数
的定义域为R,若存在常数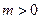 ,使
,使 对一切实数
对一切实数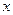 均成立,则称
均成立,则称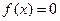 ;②
;②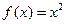 ;③
;③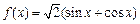 ;④
;④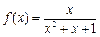 ;⑤
;⑤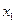 ,
,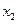 均有
均有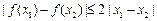 .其中是“倍约束函数”的序号是
.其中是“倍约束函数”的序号是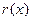 (件)与衬衣标价x(元/件)在销售旺季近似地符合函数关系:
(件)与衬衣标价x(元/件)在销售旺季近似地符合函数关系: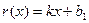 ;在销售淡季近似地符合函数关系:
;在销售淡季近似地符合函数关系: 、
、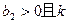 、
、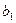 、
、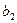 为常数;②在销售旺季,商场以140元/件的价格销售能获得最大销售利润;③若称①中
为常数;②在销售旺季,商场以140元/件的价格销售能获得最大销售利润;③若称①中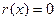 时的标价x为衬衣的“临界价格”,则销售旺季的“临界价格”是销售淡季的“临界价格”的1.5倍.
时的标价x为衬衣的“临界价格”,则销售旺季的“临界价格”是销售淡季的“临界价格”的1.5倍.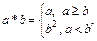 则函数
则函数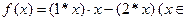
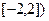 的最大值等于 .
的最大值等于 .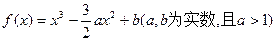 在区间
在区间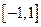 上最大值为1,最小值为
上最大值为1,最小值为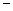 2.(1)求
2.(1)求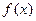 的解析式;(2)若函数
的解析式;(2)若函数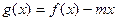 在区间
在区间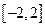 上为减函数,求实数m的取值范围.
上为减函数,求实数m的取值范围.