题目内容
设a∈R,Z1=a+2i,Z2=3-4i,且
为纯虚数,则a=
.
| Z1 |
| Z2 |
| 8 |
| 3 |
| 8 |
| 3 |
分析:利用复数的代数形式的乘除运算,将复数
的分母实数化,利用纯虚数的概念即可求得a的值.
| Z1 |
| Z2 |
解答:解:∵Z1=a+2i,Z2=3-4i,
∴
=
=
=
,
又
为纯虚数,
∴3a-8=0,
∴a=
.
当a=
时,6+4a≠0,满足题意.
故答案为:
.
∴
| Z1 |
| Z2 |
| a+2i |
| 3-4i |
| (a+2i)(3+4i) |
| (3-4i)(3+4i) |
| (3a-8)+(6+4a)i |
| 25 |
又
| Z1 |
| Z2 |
∴3a-8=0,
∴a=
| 8 |
| 3 |
当a=
| 8 |
| 3 |
故答案为:
| 8 |
| 3 |
点评:本题考查复数的代数形式的乘除运算,将复数
的分母实数化是关键,考查分析与运算能力,属于中档题.
| Z1 |
| Z2 |

练习册系列答案
相关题目
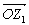 分别对应复数z1、z2,且z1=
分别对应复数z1、z2,且z1=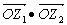 的值.
的值.