题目内容
如图,已知BC是半径为1的半圆O的直径,A是半圆周上不同于B,C的点,F为
的中点.梯形ACDE中,DE∥AC,且AC=2DE,平面ACDE⊥平面ABC.求证:
(1)平面ABE⊥平面ACDE;
(2)平面OFD∥平面BAE.
 |
| AC |
(1)平面ABE⊥平面ACDE;
(2)平面OFD∥平面BAE.

证明:(1)∵BC是半圆O的直径,A是半圆周上不同于B,C的点AC
∴∠BAC=90°,∴AC⊥AB
∵平面ACDE⊥平面ABC,平面ACDE∩平面ABC=AC,AB?平面ABC
∴由两个平面垂直的性质得,AB⊥平面ACDE
∵AB?平面ABE
∴平面ABE⊥平面ACDE.
(2)

如图,设OF∩AC=M,连接DM,OA
∵F为
的中点
∴M为AC的中点.
∵AC=2DE,DE∥AC
∴DE∥AM,DE=AM
∴四边形AMDE为平行四边形.
∴DM∥AE
∵DM?平面ABE,AE?平面ABE
∴DM∥平面ABE
∵O为BC中点
∴OM为三角形ABC的中位线
∴OM∥AB
∵OM?平面ABE,AB?平面ABE
∴OM∥平面ABE
∵OM?平面OFD,DM?平面OFD,OM∩DM=M
∴由两个平面平行的判定定理可知,平面OFD∥平面ABE.
∴∠BAC=90°,∴AC⊥AB
∵平面ACDE⊥平面ABC,平面ACDE∩平面ABC=AC,AB?平面ABC
∴由两个平面垂直的性质得,AB⊥平面ACDE
∵AB?平面ABE
∴平面ABE⊥平面ACDE.
(2)

如图,设OF∩AC=M,连接DM,OA
∵F为
 |
| AC |
∴M为AC的中点.
∵AC=2DE,DE∥AC
∴DE∥AM,DE=AM
∴四边形AMDE为平行四边形.
∴DM∥AE
∵DM?平面ABE,AE?平面ABE
∴DM∥平面ABE
∵O为BC中点
∴OM为三角形ABC的中位线
∴OM∥AB
∵OM?平面ABE,AB?平面ABE
∴OM∥平面ABE
∵OM?平面OFD,DM?平面OFD,OM∩DM=M
∴由两个平面平行的判定定理可知,平面OFD∥平面ABE.

练习册系列答案
相关题目
 (2012•蓝山县模拟)如图,已知BC是半径为1的半圆O的直径,A是半圆周上不同于B,C的点,F为
(2012•蓝山县模拟)如图,已知BC是半径为1的半圆O的直径,A是半圆周上不同于B,C的点,F为
 如图,已知BC是半径为1的半圆O的直径,A是半圆周上不同于B,C的点,又DC⊥面ABC,四边形ACDE为梯形,DE∥AC,且AC=2DE,DC=2,二面角B-DE-C的大小为θ,tan
如图,已知BC是半径为1的半圆O的直径,A是半圆周上不同于B,C的点,又DC⊥面ABC,四边形ACDE为梯形,DE∥AC,且AC=2DE,DC=2,二面角B-DE-C的大小为θ,tan 如图,已知BC是半径为1的半圆O的直径,A是半圆周上不同于B,C的点,F为
如图,已知BC是半径为1的半圆O的直径,A是半圆周上不同于B,C的点,F为 的中点.梯形ACDE中,DE∥AC,且AC=2DE,平面ACDE⊥平面ABC.求证:
的中点.梯形ACDE中,DE∥AC,且AC=2DE,平面ACDE⊥平面ABC.求证: 的中点.梯形ACDE中,DE∥AC,且AC=2DE,平面ACDE⊥平面ABC.求证:
的中点.梯形ACDE中,DE∥AC,且AC=2DE,平面ACDE⊥平面ABC.求证:
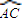 的中点.梯形ACDE中,DE∥AC,且AC=2DE,平面ACDE⊥平面ABC.求证:
的中点.梯形ACDE中,DE∥AC,且AC=2DE,平面ACDE⊥平面ABC.求证: