题目内容

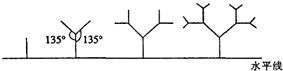
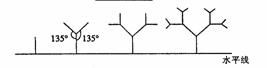
如图所示，一种树形图为：第一层是一条与水平线垂直的线段，长度为第二层在第一层线段的前端作两条与其成135°角的线段，长度为其一半；第三层按第二层的方法在每一条线段的前端生成两条线段．重复前面的作法作图至第《层，设树形的第n层的最高点至水平线的距离为第W层的树形的总高度，则到第四层的树形图的总高度h₄=________，当n为偶数时，到第《层的树形图的总高度h_n=________

$\text{[math]}$ $\text{[math]}$
分析：根据树形图的规则，可先求出第一层的最高点到水平线的距离为h₁=1米；第二层的最高点到水平线的距离为h₂=1+ $\text{[math]}$ ；第三层的最高点到水平线的距离为h₃=1+ $\text{[math]}$ + $\text{[math]}$ ；第四层的最高点到水平线的距离为h₄=1+ $\text{[math]}$ + $\text{[math]}$ + $\text{[math]}$ ，从而可求当n为偶数时，到第W层的树形图的总高度h_n=1+ $\text{[math]}$ + $\text{[math]}$ + $\text{[math]}$ +…+ $\text{[math]}$
，故可得结论
解答：第一层的最高点到水平线的距离为h₁=1米；
第二层的最高点到水平线的距离为h₂=1+ $\text{[math]}$ ；
第三层的最高点到水平线的距离为h₃=1+ $\text{[math]}$ + $\text{[math]}$ ；
第四层的最高点到水平线的距离为h₄=1+ $\text{[math]}$ + $\text{[math]}$ + $\text{[math]}$ = $\text{[math]}$ ；
推而广之，当n为偶数时，到第W层的树形图的总高度h_n=1+ $\text{[math]}$ + $\text{[math]}$ + $\text{[math]}$ +…+ $\text{[math]}$
=（1+ $\text{[math]}$ +…+ $\text{[math]}$ ）+（ $\text{[math]}$ + $\text{[math]}$ +…+ $\text{[math]}$ ）= $\text{[math]}$
= $\text{[math]}$ ；
故答案为 $\text{[math]}$ ； $\text{[math]}$ ．
点评：本题重点考查归纳推理，考查学生分析解决问题的能力，考查学生对新规则的理解，属于基础题．

练习册系列答案

，当n为偶数时，到第《层的树形图的总高度h_n=

如图所示，一种树形图为：第一层是一条与水平线垂直的线段，长度为1；第二层在第一层线段的前端作两条与其成角的线段，长度为其一半；第三层按第二层的方法在每一条线段的前端生成两条线段，重复前面的作法作图至第层，设树形的第层的最高点至水平线的距离为第层的树形的总高度，则到第四层的树形图的总高度，当为偶数时，到第层的树形图的总高度。

试题分类