题目内容
 如图,菱形ABCD的边长为1,有∠D=120°,点E、F分别是AD、DC的中点,BE、BF分别与AC交于点M、N.
如图,菱形ABCD的边长为1,有∠D=120°,点E、F分别是AD、DC的中点,BE、BF分别与AC交于点M、N.
(1)求AC的值.
(2)求MN的值.
解:(1)连接BD交AC于点O,由∠ADC=120°,得∠ADO=60°,
而∠AOD=90°,AD=1,得 ,
, ,∴
,∴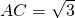 ;
;
(2)设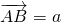 ,
, ,则
,则 ,而B、M、E三点共线,
,而B、M、E三点共线,
∴ ,即
,即 ,∴
,∴ ,
,
即 ,有
,有 ,解得
,解得 ,
,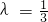 ,
,
∴ ,即
,即 ,同理
,同理 ,得
,得
由(1)得 ,∴
,∴ .
.
即 .
.
分析:(1)利用菱形的对角线垂直及对角线平分顶角,再解直角三角形求出边AC
(2)利用三点共线则向量共线,据向量共线的充要条件设出 共线的条件及
共线的条件及 共线的条件,
共线的条件,
两等式联立求出点M所在的位置,同理得到点N的位置,求出|MN|的长.
点评:本题考查菱形的对角线的性质、向量共线的充要条件、向量的运算律及运算法则.
而∠AOD=90°,AD=1,得
 ,
, ,∴
,∴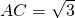 ;
;(2)设
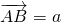 ,
, ,则
,则 ,而B、M、E三点共线,
,而B、M、E三点共线,∴
 ,即
,即 ,∴
,∴ ,
,即
 ,有
,有 ,解得
,解得 ,
,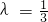 ,
,∴
 ,即
,即 ,同理
,同理 ,得
,得
由(1)得
 ,∴
,∴ .
.即
 .
.分析:(1)利用菱形的对角线垂直及对角线平分顶角,再解直角三角形求出边AC
(2)利用三点共线则向量共线,据向量共线的充要条件设出
 共线的条件及
共线的条件及 共线的条件,
共线的条件,两等式联立求出点M所在的位置,同理得到点N的位置,求出|MN|的长.
点评:本题考查菱形的对角线的性质、向量共线的充要条件、向量的运算律及运算法则.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
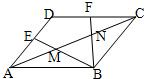 如图,菱形ABCD的边长为1,有∠D=120°,点E、F分别是AD、DC的中点,BE、BF分别与AC交于点M、N.
如图,菱形ABCD的边长为1,有∠D=120°,点E、F分别是AD、DC的中点,BE、BF分别与AC交于点M、N. (2011•西城区二模)如图,菱形ABCD的边长为6,∠BAD=60°,AC∩BD=O.将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点,
(2011•西城区二模)如图,菱形ABCD的边长为6,∠BAD=60°,AC∩BD=O.将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点, 如图,菱形ABCD的边长为4,∠BAD=60°,AC∪BD=O.将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点,DM=2
如图,菱形ABCD的边长为4,∠BAD=60°,AC∪BD=O.将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点,DM=2 如图,菱形ABCD的边长为4,∠BAD=60°,AC∩BD=O.将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点,DM=
如图,菱形ABCD的边长为4,∠BAD=60°,AC∩BD=O.将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点,DM= 如图,菱形ABCD的边长为2,∠A=60°,M为DC的中点,若N为菱形内任意一点(含边界),则
如图,菱形ABCD的边长为2,∠A=60°,M为DC的中点,若N为菱形内任意一点(含边界),则