题目内容
某厂要生产甲、乙两种产品,甲产品每单位需A种原料8 g,B种原料24 g,每单位利润60元;乙产品每单位需A种原料16 g,B种原料16 g,每单位利润80元.现A种原料库存量为2 400 g,B种原料库存量为2 880 g.问甲、乙两种产品各生产多少单位,工厂可获得最大利润?(原料不再外购,产品可完全售出)
解析:设生产甲、乙两种产品分别为x单位、y单位,所获利润为z元,依题意有
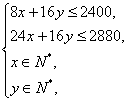z=60x+80y.
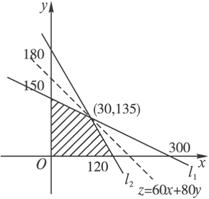
分别作出直线l1:8x+16y=2 400,l2:24x+16y=2 880.
画出8x+16y≤2 400,24x+16y≤2 800以及x＞0,y＞0
在平面上表示的区域,如图所示.
由
解得
交点为M(30,135).
再由z=60x+80y,知y=-
x+
.
∴z的最大值即由直线y=-
x+
在y轴上的截距的最大值确定,在上图的可行域内,其过点M(30,135)时,z最大.
∴zmax=60×30+80×135=12 600(元).
故当工厂生产甲产品30单位,生产乙产品135单位时,可获得最大利润.
练习册系列答案
相关题目
某厂生产甲产品每千克需用原料A和原料B分别为a1、b1千克，生产乙产品每千克需用原料A和原料B分别为a2、b2千克．甲、乙产品每千克可获利润分别为d1、d2元．月初一次性购进本月用原料A、B各c1、c2千克．要计划本月生产甲、乙两种产品各多少千克才能使月利润总额达到最大．在这个问题中，设全月生产甲、乙两种产品分别为x千克、y千克，月利润总额为z元，那么，用于求使总利润z=d1x+d2y最大的数学模型中，约束条件为（ ）
A、
| |||||||
B、
| |||||||
C、
| |||||||
D、
|