Question

在平面几何里，已知Rt_△SAB的两边SA，SB互相垂直，且SA=a，SB=b，则AB边上的高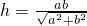；现在把结论类比到空间：三棱锥S-ABC的三条侧棱SA，SB，SC两两相互垂直，SH⊥平面ABC，且SA=a，SB=b，SC=c，则点S到平面ABC的距离h'=________．

Answer 1

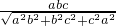
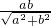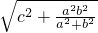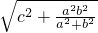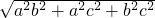分析：设S到平面ABC的距离为h，过点S向底面ABC引垂线，垂足为O，连CO并延长交AB于M，连接SM，则SM⊥AB，CM⊥AB，在直角三角形SAB中可求得AB=，SM=，同理在直角三角形CSM中可求得|CM|=，于是S_△ABC=•|AB|•|CM|=••=•，由V_S-ABC=V_C-ABS，即可求得S到平面ABC的距离为h′．
解答：把结论类比到空间：三棱锥S-ABC的三条侧棱SA，SB，SC两两相互垂直，SH⊥平面ABC，且SA=a，SB=b，SC=c，则点S到平面ABC的距离h'=．
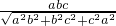证明：设S到平面ABC的距离为h′，过点S向底面ABC引垂线，垂足为O，连CO并延长交AB于M，连接SM，则SM⊥AB，CM⊥AB，
在直角三角形SAB中，由勾股定理得|AB|=，又ab=|AB|•|SM|
∴|SM|=，
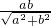∵SA，SB，SC两两相互垂直，故SC⊥平面SAB，SM?平面SAB，
∴SC⊥SM，
∵在直角三角形CSM中，|CM|=，
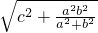∴是S_△ABC=•|AB|•|CM|=••=•，
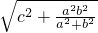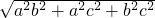由V_S-ABC=V_C-ABS可得：
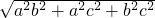•abc=S_△ABC•h′=•••h′，
∴h′=，
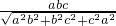∴S到平面ABC的距离h′=．
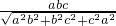故答案为：．
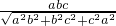点评：本题考查类比推理，难点在于线面垂直（SC⊥平面SAB）的性质（SC⊥SM）的应用，着重考查类比推理的思想及等体积轮换公式的应用，属于中档题．