题目内容
【题目】关于x的不等式ax2﹣|x+1|+3a≥0的解集为(﹣∞,+∞),则实数a的取值范围是 .
【答案】[ ![]() ,+∞)
,+∞)
【解析】解:不等式ax2﹣|x+1|+3a≥0,
则a(x2+3)≥|x+1|,
即a≥ ![]() ,
,
设t=x+1,则x=t﹣1,
则不等式a≥ ![]() 等价为a≥
等价为a≥ ![]() =
= ![]() =
= ![]() >0
>0
即a>0,
设f(t)= ![]() ,
,
当|t|=0,即x=﹣1时,不等式等价为a+3a=4a≥0,此时满足条件,
当t>0,f(t)= ![]() =
= 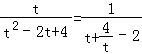
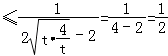 ,当且仅当t=
,当且仅当t= ![]() ,
,
即t=2,即x=1时取等号.
当t<0,f(t)= ![]() =
= 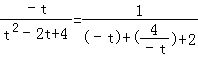 ≤
≤ 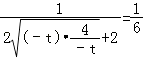 ,
,
当且仅当﹣t=﹣ ![]() ,
,
∴t=﹣2,即x=﹣3时取等号.
∴当x=1,即t=2时,fmax(t)= ![]() =
= ![]() ,
,
∴要使a≥ ![]() 恒成立,则a
恒成立,则a ![]() ,
,
方法2:由不等式ax2﹣|x+1|+3a≥0,
则a(x2+3)≥|x+1|,
∴要使不等式的解集是(﹣∞,+∞),则a>0,
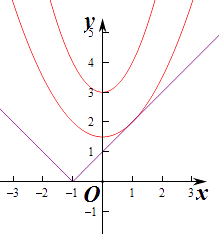
作出y=a(x2+3)和y=|x+1|的图象,
由图象知只要当x>﹣1时,直线y═|x+1|=x+1与y=a(x2+3)相切或相离即可,
此时不等式ax2﹣|x+1|+3a≥0等价为不等式ax2﹣x﹣1+3a≥0,
对应的判别式△=1﹣4a(3a﹣1)≤0,
即﹣12a2+4a+1≤0,
即12a2﹣4a﹣1≥0,
(2a﹣1)(6a+1)≥0,
解得a≥ ![]() 或a≤﹣
或a≤﹣ ![]() (舍),
(舍),
故答案为:[ ![]() ,+∞)
,+∞)
将不等式恒成立进行参数分类得到a≥ ![]() ,利用换元法将不等式转化为基本不等式的性质,根据基本不等式的性质求出
,利用换元法将不等式转化为基本不等式的性质,根据基本不等式的性质求出 ![]() 的最大值即可得到结论.
的最大值即可得到结论.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目