题目内容
已知幂函数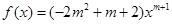 为偶函数.
为偶函数.
(1)求 的解析式;
的解析式;
(2)若函数 在区间(2,3)上为单调函数,求实数
在区间(2,3)上为单调函数,求实数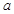 的取值范围.
的取值范围.
(1)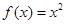 ;(2)
;(2)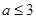 或
或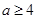
解析试题分析:(1)因为函数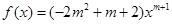 为幂函数,所以
为幂函数,所以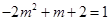 ,所以解得
,所以解得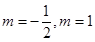 .所以函数
.所以函数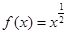 或
或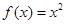 .又因为函数
.又因为函数 为偶函数,所以函数
为偶函数,所以函数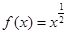 不符合舍去.所以
不符合舍去.所以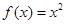 .本小题关键是考查幂函数的概念.
.本小题关键是考查幂函数的概念.
(2)由(1)得函数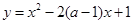 .因为二次函数的对称轴
.因为二次函数的对称轴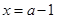 .又因为函数
.又因为函数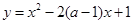 在区间(2,3)上为单调函数.所以函数的对称轴在区间(2,3)外面所以得到两个不等式即可求得
在区间(2,3)上为单调函数.所以函数的对称轴在区间(2,3)外面所以得到两个不等式即可求得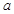 的范围.
的范围.
试题解析:(1)由 为幂函数知
为幂函数知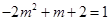 ,得
,得 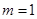 或
或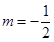 3分
3分
当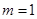 时,
时,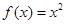 ,符合题意;当
,符合题意;当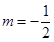 时,
时,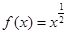 ,不合题意,舍去.
,不合题意,舍去.
∴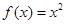 . 6分
. 6分
(2)由(1)得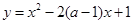 ,
,
即函数的对称轴为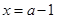 , 8分
, 8分
由题意知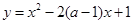 在(2,3)上为单调函数,
在(2,3)上为单调函数,
所以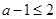 或
或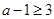 , 11分
, 11分
即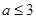 或
或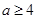 . 12分
. 12分
考点:1.基本初等函数的一般式.2.二次函数的单调性.

练习册系列答案
相关题目
 -
- +1的最小值与最大值.
+1的最小值与最大值. 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时, .
. ;
; ,求区间
,求区间 .
. +2+a(ω>0,a∈R),且f(x)的图象在y轴右侧的第一个最高点的横坐标为2.
+2+a(ω>0,a∈R),且f(x)的图象在y轴右侧的第一个最高点的横坐标为2.
 的单调区间;
的单调区间; (
( )在
)在 上恒成立,求
上恒成立,求 的最大值.
的最大值. 且
且 的图象经过点
的图象经过点 .
.  的解析式;
的解析式; ,用函数单调性的定义证明:函数
,用函数单调性的定义证明:函数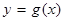 在区间
在区间 上单调递减;
上单调递减; .
. .
. 的定义域;
的定义域; ,求
,求 的取值范围.
的取值范围. 与第x天近似地满足
与第x天近似地满足 (千人),且参观民俗文化村的游客人均消费
(千人),且参观民俗文化村的游客人均消费 近似地满足
近似地满足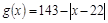 (元).
(元).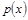 (单位千元,1≤x≤30,
(单位千元,1≤x≤30,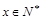 )的函数关系;
)的函数关系;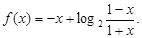
 的定义域;
的定义域;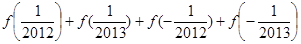 的值;
的值;