题目内容
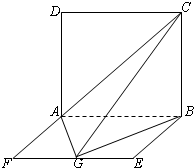 如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且AF=
如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且AF=| 1 | 2 |
(Ⅰ)求证:平面AGC⊥平面BGC;
(Ⅱ)求三棱锥A-GBC的体积.
分析:(I)由G是矩形ABEF的边EF的中点,我们由已知中ABEF是矩形,且AF=
AD=2,得到AG,及BG的长,根据勾股定理,我们可得到AG⊥BG,又由平面ABCD⊥平面ABEF,ABCD是正方形,结合面面垂直的性质,我们易得到BC⊥平面ABEF,进而由线面垂直的定义得到BC⊥AG,由线面垂直及面百垂直的判定定理,即可得到平面AGC⊥平面BGC;
(Ⅱ)由(I)中结论,我们易得到三棱锥A-GBC中以CB为高,在三角形ABG为底的三棱锥,求出底面面积和高后,代入棱锥体积公式即可得到答案.
| 1 |
| 2 |
(Ⅱ)由(I)中结论,我们易得到三棱锥A-GBC中以CB为高,在三角形ABG为底的三棱锥,求出底面面积和高后,代入棱锥体积公式即可得到答案.
解答:证明:(I)∵G是矩形ABEF的边EF的中点
∴AG=BG=
=2
∴AG2+BG2=AB2
∴AG⊥BG
又∵平面ABCD⊥平面ABEF,平面ABCD∩平面ABEF=AB,
且BC⊥AB
∴BC⊥平面ABEF,
又∵AG?平面ABEF,
∴BC⊥AG
∵BC∩BG=B
∴AG⊥平面BGC
∵AG?平面AGC
∴平面AGC⊥平面BGC;
解:(Ⅱ)由(I)得知:直线BC⊥平面ABEF
∴CB是三棱锥的高
而S△ABG=
×2
×2
∴VA-GBC=VC-ABG=
×4×4=
∴AG=BG=
| 22+22 |
| 2 |
∴AG2+BG2=AB2
∴AG⊥BG
又∵平面ABCD⊥平面ABEF,平面ABCD∩平面ABEF=AB,
且BC⊥AB
∴BC⊥平面ABEF,
又∵AG?平面ABEF,
∴BC⊥AG
∵BC∩BG=B
∴AG⊥平面BGC
∵AG?平面AGC
∴平面AGC⊥平面BGC;
解:(Ⅱ)由(I)得知:直线BC⊥平面ABEF
∴CB是三棱锥的高
而S△ABG=
| 1 |
| 2 |
| 2 |
| 2 |
∴VA-GBC=VC-ABG=
| 1 |
| 3 |
| 16 |
| 3 |
点评:本题考查的知识点是平面与平面垂直的判定,棱锥的体积,其中熟练掌握空间线线垂直、线面垂直、面面垂直之间的转化是证明本题结论的重要环节.

练习册系列答案
相关题目
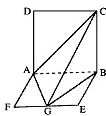 如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且AF=
如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且AF= 如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且
如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且 (2010•河东区一模)如图,平面ABCD⊥平面ABEF,ABCD是正方形.ABEF是矩形,G是线段EF的中点,且B点在平面ACG内的射影在CG上.
(2010•河东区一模)如图,平面ABCD⊥平面ABEF,ABCD是正方形.ABEF是矩形,G是线段EF的中点,且B点在平面ACG内的射影在CG上.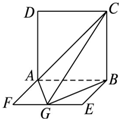 如图,平面ABCD⊥平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,且AF=
如图,平面ABCD⊥平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,且AF=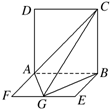 如图,平面ABCD⊥平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,且AF=
如图,平面ABCD⊥平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,且AF=