题目内容
在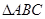 中,角
中,角 所对的边分别为
所对的边分别为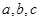 ,且满足
,且满足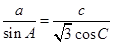 .
.
(1)求角 的大小;
的大小;
(2)求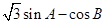 的最大值,并求此时角
的最大值,并求此时角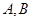 的大小.
的大小.
(1) (2)最大值为1, 此时
(2)最大值为1, 此时 .
.
解析试题分析:解:(1)由条件结合正弦定理得, ,从而
,从而 ,
, , ∵
, ∵ ,∴
,∴ ;
;
(2)由(1)知 ,∴
,∴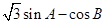




∵ ,∴
,∴ ,当
,当 时,
时,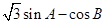 取得最大值为1, 此时
取得最大值为1, 此时 .
.
考点:正弦定理;三角恒等变换
点评:关于三角函数的题目,要求出一个式子的最值,像本题是要求出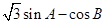 的最大值,则需将式子化为
的最大值,则需将式子化为 的形式。
的形式。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,c.已知
,c.已知 .
.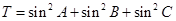 ,求T的取值范围.
,求T的取值范围. ,
,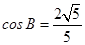 .
. ,D为AB的中点,求CD的长.
,D为AB的中点,求CD的长. 中,角
中,角 的对边分别是
的对边分别是 ,且
,且
 的大小:
的大小: 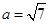 ,且
,且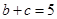 ,求
,求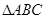 的内角
的内角 所对边分别为
所对边分别为 ,且
,且 .
. 的大小;
的大小; ,求边长
,求边长 的最小值.
的最小值.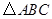 中,内角
中,内角 对边的边长分别是
对边的边长分别是 ,已知
,已知 ,
, .
. ,求
,求 ;
; ,求
,求 的两个根, 且
的两个根, 且 。求:(1)角C的度数; (2)AB的长度。
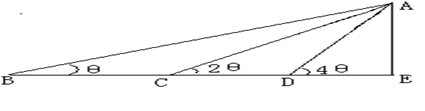
。求:(1)角C的度数; (2)AB的长度。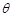 ,沿BE方向前进30m,至点C处测得顶端A的仰角为2
,沿BE方向前进30m,至点C处测得顶端A的仰角为2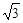 m至D点,测得顶端A的仰角为4
m至D点,测得顶端A的仰角为4