题目内容
已知函数y=Asin(ωx+φ)+m的最大值为4,最小值为0,最小正周期为2,直线 是其图象的一条对称轴,则下面各式中符合条件的解析式是( )
是其图象的一条对称轴,则下面各式中符合条件的解析式是( )A.

B.

C.

D.

【答案】分析:由 可求得A,m;由T=
可求得A,m;由T= ,可求得ω,由直线
,可求得ω,由直线 是其图象的一条对称轴,可知当x=
是其图象的一条对称轴,可知当x= 时,y能取到最值,从而可得符合条件的φ,从而可得满足条件的解析式.
时,y能取到最值,从而可得符合条件的φ,从而可得满足条件的解析式.
解答:解:∵函数y=Asin(ωx+φ)+m的最大值为4,最小值为0,
∴ 解得A=2,m=2;
解得A=2,m=2;
∵其最小正周期为2,∴ ,∴ω=π;
,∴ω=π;
又直线 是其图象的一条对称轴,
是其图象的一条对称轴,
∴ ,φ=kπ+
,φ=kπ+ (k∈Z),
(k∈Z),
所求函数的解析式为:y=2sin(πx+kπ+ )+2,
)+2,
当k=0时,解析式为: .
.
故选B.
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,关键是A,ω,φ,m的确定,属于中档题.
 可求得A,m;由T=
可求得A,m;由T= ,可求得ω,由直线
,可求得ω,由直线 是其图象的一条对称轴,可知当x=
是其图象的一条对称轴,可知当x= 时,y能取到最值,从而可得符合条件的φ,从而可得满足条件的解析式.
时,y能取到最值,从而可得符合条件的φ,从而可得满足条件的解析式.解答:解:∵函数y=Asin(ωx+φ)+m的最大值为4,最小值为0,
∴
 解得A=2,m=2;
解得A=2,m=2;∵其最小正周期为2,∴
 ,∴ω=π;
,∴ω=π;又直线
 是其图象的一条对称轴,
是其图象的一条对称轴,∴
 ,φ=kπ+
,φ=kπ+ (k∈Z),
(k∈Z),所求函数的解析式为:y=2sin(πx+kπ+
 )+2,
)+2,当k=0时,解析式为:
 .
.故选B.
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,关键是A,ω,φ,m的确定,属于中档题.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
已知函数y=Asin(ωx+φ),在同一周期内,当x=
时,取最大值y=2,当x=
时,取得最小值y=-2,那么函数的解析式为( )
| π |
| 12 |
| 7π |
| 12 |
A、y=
| ||||
B、y=2sin(2x+
| ||||
C、y=2sin(
| ||||
D、y=2sin(2x+
|
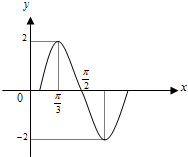 已知函数y=Asin(ωx+∅)(A>0,ω>0,-π≤∅≤π)一个周期的图象(如图),则这个函数的一个解析式为( )
已知函数y=Asin(ωx+∅)(A>0,ω>0,-π≤∅≤π)一个周期的图象(如图),则这个函数的一个解析式为( )A、y=2sin(
| ||||
B、y=2sin(3x+
| ||||
C、y=2sin(3x-
| ||||
D、y=2sin(3x-
|
 已知函数
已知函数 已知函数
已知函数