题目内容
设数列{an}的前n项和Sn=2an+ ×(-1)n-
×(-1)n- ,n∈N*.
,n∈N*.
(Ⅰ)求an和an-1的关系式;
(Ⅱ)求数列{an}的通项公式;
(Ⅲ)证明: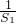 +
+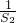 +…+
+…+ <
< ,n∈N*.
,n∈N*.
解:(Ⅰ)由Sn=2an+ ×(-1)n-
×(-1)n- ,n=1,2,3,…,①
,n=1,2,3,…,①
得Sn-1=2an-1+ ×(-1)n-1-
×(-1)n-1- ,n=2,3,…,②
,n=2,3,…,②
将①和②相减得: ,n=2,3,…,
,n=2,3,…,
整理得:an=2an-1+3×(-1)n-1,n=2,3,….
(Ⅱ)在已知条件中取n=1得,a1=2a1- -
- ,∴a1═2.
,∴a1═2.
∵an=2an-1+3×(-1)n-1,∴(-1)nan=-2(-1)n-1an-1-3,
∴令bn=(-1)nan得bn=-2bn-1-3,n=2,3,….
∴bn+1+1=-2(bn+1),n=1,2,3,…,
∵b1+1=-1≠0,∴bn+1=(-1)×(-2)n-1,n=1,2,3,…,
∴an=2n-1+(-1)n-1.
(Ⅲ)∵ ,∴S2k-1=22k-1,S2k=22k-1.
,∴S2k-1=22k-1,S2k=22k-1.
∴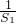 +
+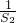 +…+
+…+ =
= <
< .
.
同理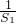 +
+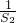 +…+
+…+
 ,∴
,∴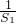 +
+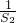 +…+
+…+ <
< ,n∈N*.
,n∈N*.
分析:(Ⅰ)由Sn=2an+ ×(-1)n-
×(-1)n- ,n=1,2,3,…,再写一式,两式相减整理可得an=2an-1+3×(-1)n-1
,n=1,2,3,…,再写一式,两式相减整理可得an=2an-1+3×(-1)n-1
(Ⅱ)由(Ⅰ)令bn=(-1)nan得bn=-2bn-1-3,构造新数列bn+1是等比数列,从而可求数列{an}的通项公式;
(Ⅲ)由 ,∴S2k-1=22k-1,S2k=22k-1,再进行分组求和,利用等比数列的求和公式可证.
,∴S2k-1=22k-1,S2k=22k-1,再进行分组求和,利用等比数列的求和公式可证.
点评:本题主要考查数列通项公式的求解,考查数列与不等式的综合,有一定的难度.
 ×(-1)n-
×(-1)n- ,n=1,2,3,…,①
,n=1,2,3,…,①得Sn-1=2an-1+
 ×(-1)n-1-
×(-1)n-1- ,n=2,3,…,②
,n=2,3,…,②将①和②相减得:
 ,n=2,3,…,
,n=2,3,…,整理得:an=2an-1+3×(-1)n-1,n=2,3,….
(Ⅱ)在已知条件中取n=1得,a1=2a1-
 -
- ,∴a1═2.
,∴a1═2.∵an=2an-1+3×(-1)n-1,∴(-1)nan=-2(-1)n-1an-1-3,
∴令bn=(-1)nan得bn=-2bn-1-3,n=2,3,….
∴bn+1+1=-2(bn+1),n=1,2,3,…,
∵b1+1=-1≠0,∴bn+1=(-1)×(-2)n-1,n=1,2,3,…,
∴an=2n-1+(-1)n-1.
(Ⅲ)∵
 ,∴S2k-1=22k-1,S2k=22k-1.
,∴S2k-1=22k-1,S2k=22k-1.∴
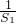 +
+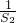 +…+
+…+ =
= <
< .
.同理
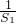 +
+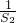 +…+
+…+
 ,∴
,∴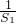 +
+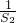 +…+
+…+ <
< ,n∈N*.
,n∈N*.分析:(Ⅰ)由Sn=2an+
 ×(-1)n-
×(-1)n- ,n=1,2,3,…,再写一式,两式相减整理可得an=2an-1+3×(-1)n-1
,n=1,2,3,…,再写一式,两式相减整理可得an=2an-1+3×(-1)n-1(Ⅱ)由(Ⅰ)令bn=(-1)nan得bn=-2bn-1-3,构造新数列bn+1是等比数列,从而可求数列{an}的通项公式;
(Ⅲ)由
 ,∴S2k-1=22k-1,S2k=22k-1,再进行分组求和,利用等比数列的求和公式可证.
,∴S2k-1=22k-1,S2k=22k-1,再进行分组求和,利用等比数列的求和公式可证.点评:本题主要考查数列通项公式的求解,考查数列与不等式的综合,有一定的难度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目