Question

设f（x）=x³+x²-3x+5
（1）求函数f（x）的单调递增区间、递减区间；
（2）当x∈[-1，2]时，求函数的最值．

Answer 1

解：（1）由题意，f′（x）=（x+3）（x-1）------------------------------（2分）
当x∈（-∞，-3）时，f′（x）＞0；
当x∈（-3，1）时，f′（x）＜0；
当x∈（3，+∞）时，f′（x）＞0．-----------------------------（4分）
所以，函数f（x）的单调递增区间为（-∞，-3）和（3，+∞）、递减区间（-3，1）------（6分）
（2）当x变化时，f′（x），f（x）的变化情况如下表

x	-1	（-1，1）	1	（1，2）	2
f′（x）		-	0	+
f（x）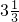

--------------（10分）
所以，当x=-1，
当x=1，------------------------------（12分）
分析：（1）先求导函数，利用导数大于0，可得函数的单调增区间；导数小于0，可得函数的单调增区间；
（2）令导数等于0，确定函数的极值点，再考虑端点的函数值，从而确定函数的最值．
点评：本题以函数为载体，考查函数的单调性，考查函数的最值，关键是正确运用导数工具．