题目内容
(8分)已知函数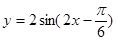 .
.
(1)写出它的振幅、周期、频率和初相;
(2)求这个函数的单调递减区间;
(3)求出使这个函数取得最大值时,自变量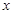 的取值集合,并写出最大值。
的取值集合,并写出最大值。
(1)振幅2,周期 ,频率
,频率 ,初相
,初相 (2)
(2)
(3)当 ,函数有最大值
,函数有最大值
解析试题分析:(1)振幅2,周期 ,频率
,频率 ,初相
,初相 (2)令
(2)令 整理得
整理得 (3)函数最大值为2,此时需满足
(3)函数最大值为2,此时需满足
考点:三角函数性质
点评:三角函数 最值由振幅A决定,周期由
最值由振幅A决定,周期由 决定,平移由
决定,平移由 决定,求增区间令
决定,求增区间令 ,求减区间令
,求减区间令 ,在高考题中已知条件常给出一个较复杂的三角函数式,需要考生利用诱导公式,和差角的正余弦公式,二倍角公式等将其化简为
,在高考题中已知条件常给出一个较复杂的三角函数式,需要考生利用诱导公式,和差角的正余弦公式,二倍角公式等将其化简为 的形式
的形式

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 拟合(
拟合(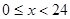 ,单位为小时,
,单位为小时, 表示气温,单位为摄氏度,
表示气温,单位为摄氏度,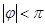 ,
,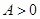 ),
),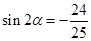 ,
,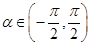 ,求
,求 的值;
的值;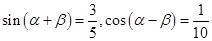 .
.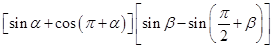 的值.
的值.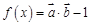 ,其中向量
,其中向量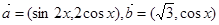 , (
, (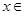 R).
R).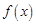 的最小正周期和最小值;
的最小正周期和最小值;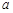 、
、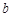 、
、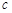 ,若
,若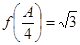 ,a=2
,a=2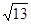 ,
,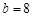 ,求边长
,求边长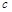 的值.
的值. =
= ,
, =
= ,其中
,其中 >0,记函数f(x)=2
>0,记函数f(x)=2 ,
,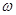 x+
x+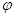 )(x∈R,
)(x∈R,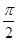 )的部分图象如图所示。
)的部分图象如图所示。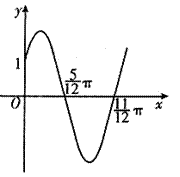
 )的单调递增区间。
)的单调递增区间。 x+
x+ )(x∈R,
)(x∈R, )的部分图象如图所示。
)的部分图象如图所示。
 )的单调递增区间。
)的单调递增区间。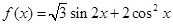 .
. 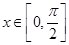 时,求函数f(x)的值域;
时,求函数f(x)的值域;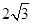 ,求a,b的值。
,求a,b的值。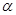 为第三象限角,
为第三象限角,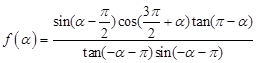 .
.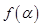 ;
;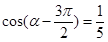 ,求
,求