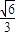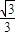题目内容
已知P、Q是椭圆 上关于原点对称的两点,M是该椭圆上任意一点,且直线MP、MQ的斜率分别为k1、k2,若
上关于原点对称的两点,M是该椭圆上任意一点,且直线MP、MQ的斜率分别为k1、k2,若 ,则椭圆的离心率为( )
,则椭圆的离心率为( )A.

B.

C.

D.

【答案】分析:先设出P,M,N的坐标,把它们代入椭圆方程,方程相减可分别表示出PM和PN的斜率,二者相乘等于 同时把x1=-x2,y1=-y2代入解求得a和b的关系,进而求得a和c的关系,则椭圆的离心率可得.
同时把x1=-x2,y1=-y2代入解求得a和b的关系,进而求得a和c的关系,则椭圆的离心率可得.
解答:解:设p(x,y),M(x1,y1),N(x2,y2),把它们代入椭圆方程得
 ①,
①, ②.
②.
②-①得PM的斜率k1= =
= ,
,
同理PN的斜率k2= =
= ,k1•k2=
,k1•k2= =
= ,
,
M、N是椭圆上关于原点对称的两点,x1=-x2,y1=-y2.
∴ =
= ,即a2=3b2,
,即a2=3b2,
∴c2=a2-b2= a2,
a2,
∴e= =
= .
.
故选C
点评:本题主要考查了椭圆的简单性质.当直线与椭圆相交时,涉及弦长中点时,或直线的斜率时都可采用点差法,设出点代入椭圆方程,然后相减,与直线的斜率和弦的中点相联系.
 同时把x1=-x2,y1=-y2代入解求得a和b的关系,进而求得a和c的关系,则椭圆的离心率可得.
同时把x1=-x2,y1=-y2代入解求得a和b的关系,进而求得a和c的关系,则椭圆的离心率可得.解答:解:设p(x,y),M(x1,y1),N(x2,y2),把它们代入椭圆方程得
 ①,
①, ②.
②.
②-①得PM的斜率k1=
 =
= ,
,同理PN的斜率k2=
 =
= ,k1•k2=
,k1•k2= =
= ,
,M、N是椭圆上关于原点对称的两点,x1=-x2,y1=-y2.
∴
 =
= ,即a2=3b2,
,即a2=3b2,∴c2=a2-b2=
 a2,
a2,∴e=
 =
= .
.故选C
点评:本题主要考查了椭圆的简单性质.当直线与椭圆相交时,涉及弦长中点时,或直线的斜率时都可采用点差法,设出点代入椭圆方程,然后相减,与直线的斜率和弦的中点相联系.

练习册系列答案
相关题目
 上关于原点对称的两点,M是该椭圆上任意一点,且直线MP、MQ的斜率分别为k1、k2,若
上关于原点对称的两点,M是该椭圆上任意一点,且直线MP、MQ的斜率分别为k1、k2,若 ,则椭圆的离心率为
,则椭圆的离心率为



 上关于原点对称的两点,M是该椭圆上任意一点,且直线MP、MQ的斜率分别为k1、k2,若
上关于原点对称的两点,M是该椭圆上任意一点,且直线MP、MQ的斜率分别为k1、k2,若 ,则椭圆的离心率为( )
,则椭圆的离心率为( )



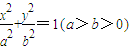 上关于原点对称的两点,M是该椭圆上任意一点,且直线MP、MQ的斜率分别为k1、k2,若
上关于原点对称的两点,M是该椭圆上任意一点,且直线MP、MQ的斜率分别为k1、k2,若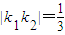 ,则椭圆的离心率为( )
,则椭圆的离心率为( )