题目内容
已知数列{an}的前n项和为Sn, ,则S2010等于 .
,则S2010等于 .
【答案】分析:因为数列{an}的前n项和为Sn,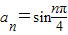 ,可得周期T=
,可得周期T=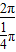 =8,求出一个周期的和,再求出S2010;
=8,求出一个周期的和,再求出S2010;
解答:解:∵数列{an}的前n项和为Sn,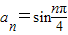 ,可得T=
,可得T=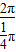 =8,
=8,
因为a1=sin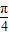 =
=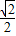 ;
;
a2=sin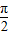 =1,
=1,
a3=sin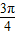 =
=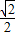 ,
,
a4=sinπ=0,
a5=sin(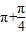 )=-
)=-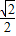 ,
,
a6=sin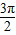 =-1,
=-1,
a7=sin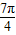 =-
=-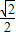 ,
,
a8=sin2π=0,一个周期为:a1+a2+a3+…+a8
=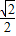 +1+
+1+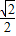 +0-
+0-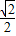 -1-
-1-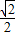 +0=0,
+0=0,
要求S2010因为2010=8×251+2,
∴S2010=251×0+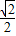 +1=
+1=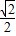 +1,
+1,
故答案为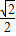 +1;
+1;
点评:此题主要考查三角函数的周期性,只要求出一个周期的和,就会比较容易,此题是一道中档题;
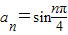 ,可得周期T=
,可得周期T=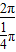 =8,求出一个周期的和,再求出S2010;
=8,求出一个周期的和,再求出S2010;解答:解:∵数列{an}的前n项和为Sn,
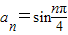 ,可得T=
,可得T=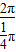 =8,
=8,因为a1=sin
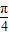 =
=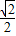 ;
;a2=sin
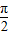 =1,
=1,a3=sin
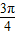 =
=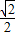 ,
,a4=sinπ=0,
a5=sin(
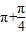 )=-
)=-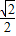 ,
,a6=sin
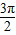 =-1,
=-1,a7=sin
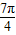 =-
=-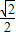 ,
,a8=sin2π=0,一个周期为:a1+a2+a3+…+a8
=
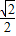 +1+
+1+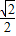 +0-
+0-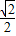 -1-
-1-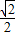 +0=0,
+0=0,要求S2010因为2010=8×251+2,
∴S2010=251×0+
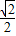 +1=
+1=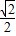 +1,
+1,故答案为
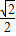 +1;
+1;点评:此题主要考查三角函数的周期性,只要求出一个周期的和,就会比较容易,此题是一道中档题;

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |