题目内容

如图，过抛物线x2 = 4y的对称轴上任一点P (0, m) (m＞0)作直线与抛物线交于A、B两点，点Q是点P关于原点的对称点.若点P满足.

证明

解：依题意,可设直线AB的方程为,

代入抛物线方程，得： … ①

设A、B两点的坐标分别是（x1,y1）、(x2, y2)，则x1、x2是方程①的两根． 所以 由，得得

又点Q是点P关于原点的对称点，故点Q的坐标是（0，m），从而

=

=

=== 0，

所以

练习册系列答案
相关题目
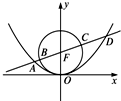精英家教网如图，过抛物线x2=4y的对称轴上任一点P（0，m）（m＞0）作直线与抛物线交于A，B两点，点Q是点P关于原点的对称点．
（I）设点P分有向线段
AB
所成的比为λ，证明：
QP
⊥(
QA
-λ
QB
)
（Ⅱ）设直线AB的方程是x-2y+12=0，过A，B两点的圆C与抛物线在点A处有共同的切线，求圆C的方程．
如图，过抛物线x2=4y的对称轴上任一点P（0，m）（m＞0）作直线与抛物线交于A（x1，y1），B（x2，y2）两点．
（I）若
AP
=λ
PB
(λ∈R)，证明：λ=-
x1
x2
；
（II）在（I）条件下，若点Q是点P关于原点对称点，证明：
QP
⊥(
QA
-λ
QB
)；
（III）设直线AB的方程是x-2y+12=0，过A，B两点的圆C与抛物线在点A处有共同的切线，求圆C的方程．
精英家教网如图，过抛物线x2=4y焦点的直线依次交抛物线与圆x2+（y-1）2=1于点A、B、C、D，则
AB
•
CD
的值是
 
．
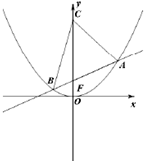（2012•绍兴模拟）如图，过抛物线x2=4y焦点F的直线l与抛物线交于A，B两点（A在第一象限），点C（0，t）（t＞1）．
（I）若△CBF，△CFA，△CBA的面积成等差数列，求直线l的方程；
（II）若|AB|∈(
9
2
，
64
7
)，且∠FAC为锐角，试求t的取值范围．
如图，过抛物线x2=4y的对称轴上任一点P（0，m）（m＞0）作直线与抛物线交于A，B两点，点Q是点P关于原点的对称点．
（I）设点P分有向线段所成的比为λ，证明：
（Ⅱ）设直线AB的方程是x-2y+12=0，过A，B两点的圆C与抛物线在点A处有共同的切线，求圆C的方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网