题目内容
甲、乙两人进行定点投篮游戏,投篮者若投中则继续投篮,否则由对方投篮,第一次由甲投篮; 已知每次投篮甲、乙命中的概率分别为 、
、 ;
;
(1)在前3次投篮中,乙投篮的次数为ξ,求Eξ;
(2)若第n次由甲投篮的概率为an,求an与an-1的关系式,并求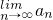 .
.
解:(1)由题意,ξ的取值为0,1,2,则
∴ξ的分布列为
∴
(2)由已知可得
∴ ,
,
∴ =
=
∴
分析:(1)确定ξ的取值,利用投蓝规则,求出相应的概率,可得分布列,从而可求Eξ;
(2)利用投蓝规则,可求an与an-1的关系式,进而可求极限.
点评:本题考查概率的计算,考查离散型随机变量的分布列与数学期望,考查数列递推式,属于中档题.

∴ξ的分布列为
| ξ | 0 | 1 | 2 |
| P |  |  |  |

(2)由已知可得

∴
 ,
,∴
 =
=
∴

分析:(1)确定ξ的取值,利用投蓝规则,求出相应的概率,可得分布列,从而可求Eξ;
(2)利用投蓝规则,可求an与an-1的关系式,进而可求极限.
点评:本题考查概率的计算,考查离散型随机变量的分布列与数学期望,考查数列递推式,属于中档题.

练习册系列答案
相关题目
 ,甲胜丙的概率为
,甲胜丙的概率为 ,乙胜丙的概率为
,乙胜丙的概率为 胜利的概率;
胜利的概率;  、
、 ,且甲、乙投篮是否命中互不影响.
,且甲、乙投篮是否命中互不影响.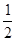 ,乙投篮一次命中的概率为
,乙投篮一次命中的概率为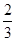 .每人各投4个球,两人投篮命中的概率互不影响.
.每人各投4个球,两人投篮命中的概率互不影响.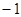 分,求乙所得分数
分,求乙所得分数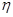 的概率分布和数学期望.
的概率分布和数学期望. ,甲胜丙的概率为
,甲胜丙的概率为 ,乙胜丙的概率为
,乙胜丙的概率为 、
、 ,且甲、乙投篮是否命中互不影响.
,且甲、乙投篮是否命中互不影响.