题目内容
已知函数f（x）=
，记f（1）+f（2）+f（4）+f（8）+…+f（1024）=m，f（
）+f（
）+f（
）+…+f（
）=n，则m+n=______．
解：f（x）+f（
）=+
=
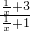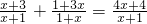=4，f（1）=
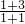=2，
则m+n=f（1）+{[f（2）+f（）]+[f（4）+f（）]+…+[f（1024）+f（）]}=2+4×10=42，
故答案为：42．
分析：先计算可找规律：f（x）+f（）=4，然后利用该结论可求答案．
点评：本题考查函数的性质及函数求值，属基础题，正确寻找规律是解决本题的关键．
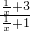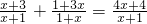）=+==4，f（1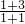）==2，则m+n=f（1）+{[f（2）+f（
）]+[f（4）+f（）]+…+[f（1024）+f（）]}=2+4×10=42，故答案为：42．
分析：先计算可找规律：f（x）+f（
）=4，然后利用该结论可求答案．点评：本题考查函数的性质及函数求值，属基础题，正确寻找规律是解决本题的关键．
练习册系列答案
相关题目
已知函数f（x）=x2-bx的图象在点A（1，f（1））处的切线l与直线3x-y+2=0平行，若数列{
}的前n项和为Sn，则S2010的值为（ ）
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|