题目内容
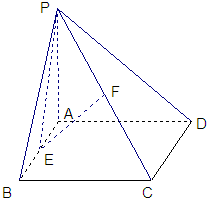
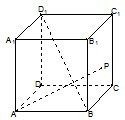
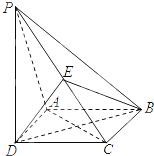
如图所示，在四棱锥P-ABCD中，底面四边形ABCD是正方形，PD⊥平面ABCD，E为PC的中点．
求证：
（1）PA∥平面BDE；
（2）AC⊥平面PBD．
求证：
（1）PA∥平面BDE；
（2）AC⊥平面PBD．
证明：（1）设AC∩BD=H，连接EH，
因为H为正方形ABCD对角线的交点，所以H为AC中点，
又E为PC中点，
所以EH为△PAC中位线，
EH∥PA，
EH?平面BDE，PA?平面BDE，
所以PA∥平面BDE．
（2）因为AC、BD为正方形ABCD的对角线，
所以AC⊥BD，
又PD⊥平面ABCD，AC?平面ABCD，
所以PD⊥AC，
又PD∩BD=D，
所以AC⊥平面PDB．
因为H为正方形ABCD对角线的交点，所以H为AC中点，
又E为PC中点，
所以EH为△PAC中位线，
EH∥PA，
EH?平面BDE，PA?平面BDE，
所以PA∥平面BDE．
（2）因为AC、BD为正方形ABCD的对角线，
所以AC⊥BD，
又PD⊥平面ABCD，AC?平面ABCD，
所以PD⊥AC，
又PD∩BD=D，
所以AC⊥平面PDB．
练习册系列答案
黄冈冠军课课练系列答案
相关题目
