题目内容
 已知函数
已知函数 的部分图象如图所示.
的部分图象如图所示.
(1)求A,ω的值;
(2)求f(x)的单调增区间;
(3)求f(x)在区间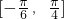 上的最大值和最小值.
上的最大值和最小值.
解:(1)由图象知A=1,…(2分)
由图象得函数的最小正周期为 ,
,
则由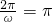 得ω=2.…(4分)
得ω=2.…(4分)
(2)∵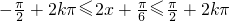 ,
,
∴ .
.
∴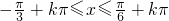 .
.
所以f(x)的单调递增区间为 .…(9分)
.…(9分)
(3)∵ ,∵
,∵ ,
,
∴ .
.
∴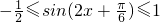 .…(12分)
.…(12分)
当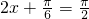 ,即
,即 时,f(x)取得最大值1;
时,f(x)取得最大值1;
当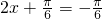 ,即
,即 时,f(x)取得最小值
时,f(x)取得最小值 .…(14分)
.…(14分)
分析:(1)通过函数的图象直接求A,利用函数的周期即可求出ω的值;
(2)根据函数的单调增区间,直接求f(x)的单调增区间即可;
(3)通过x∈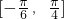 ,求出函数的相位的范围,利用正弦函数的最值,直接求解f(x)的最大值和最小值.
,求出函数的相位的范围,利用正弦函数的最值,直接求解f(x)的最大值和最小值.
点评:本题考查函数解析式的求法,正弦函数的单调性的应用,正弦函数的最值的求法,考查计算能力.
由图象得函数的最小正周期为
 ,
,则由
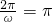 得ω=2.…(4分)
得ω=2.…(4分)(2)∵
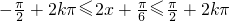 ,
,∴
 .
.∴
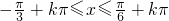 .
.所以f(x)的单调递增区间为
 .…(9分)
.…(9分)(3)∵
 ,∵
,∵ ,
,∴
 .
.∴
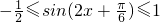 .…(12分)
.…(12分)当
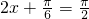 ,即
,即 时,f(x)取得最大值1;
时,f(x)取得最大值1;当
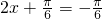 ,即
,即 时,f(x)取得最小值
时,f(x)取得最小值 .…(14分)
.…(14分)分析:(1)通过函数的图象直接求A,利用函数的周期即可求出ω的值;
(2)根据函数的单调增区间,直接求f(x)的单调增区间即可;
(3)通过x∈
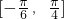 ,求出函数的相位的范围,利用正弦函数的最值,直接求解f(x)的最大值和最小值.
,求出函数的相位的范围,利用正弦函数的最值,直接求解f(x)的最大值和最小值.点评:本题考查函数解析式的求法,正弦函数的单调性的应用,正弦函数的最值的求法,考查计算能力.

练习册系列答案
相关题目
 的部分图象如右图所示,设
的部分图象如右图所示,设 是图象的最高点,
是图象的最高点, 是图象与
是图象与 轴的交点,则
轴的交点,则 ( )
( )
 B.
B.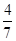 C.
C. D.
D.

 的部分图象如图所示.
的部分图象如图所示. ,判断函数g(x)的奇偶性,并说明理由.
,判断函数g(x)的奇偶性,并说明理由.
 的部分图象如图所示.
的部分图象如图所示. ,求函数f(x)的值域.
,求函数f(x)的值域.
 的部分图象如图所示,则
的部分图象如图所示,则 的解析式是 ( )
的解析式是 ( ) B.
B.
 D.
D.


 的部分图象如右图所示,则
的部分图象如右图所示,则 的值为________.
的值为________.