题目内容
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象如图所示,且f(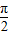 )=-
)=- ,
,(1)求函数f(x)的解析式;
(2)在锐角△ABC中,a,b,c分别是角A,B,C的对边,且f(C)=
 ,c=1,求△ABC面积的最大值.
,c=1,求△ABC面积的最大值.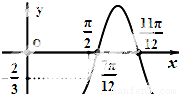
【答案】分析:(1)依题意,可求得T=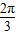 ,从而可求ω,由函数f(x)=Asin(ωx+φ)的图象经过(
,从而可求ω,由函数f(x)=Asin(ωx+φ)的图象经过(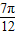 ,-
,- )及0<φ<π可求得φ,又f(
)及0<φ<π可求得φ,又f(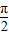 )=-
)=- 可求A;
可求A;
(2)在锐角△ABC中,由f(C)=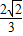 sin(3C+
sin(3C+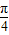 )=
)= ,可求C;利用余弦定理c2=a2+b2-2abcosC,c=1及基本不等式可求得ab≤2+
,可求C;利用余弦定理c2=a2+b2-2abcosC,c=1及基本不等式可求得ab≤2+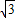 ,从而可得答案.
,从而可得答案.
解答:解:(1)由题意得,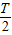 =
=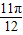 -
-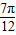 =
=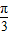 ,故T=
,故T=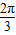 ,
,
∴ω=3…2分
又当x=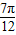 时,3x+φ=
时,3x+φ=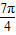 +φ=2kπ,k∈Z,
+φ=2kπ,k∈Z,
∵0<φ<π,
∴φ=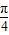 …4分
…4分
∴f(x)=Asin(3x+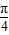 );
);
又f(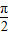 )=-
)=- ,
,
∴A=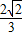 …6分
…6分
∴f(x)=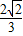 sin(3x+
sin(3x+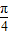 );…7分
);…7分
(2)由f(C)=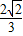 sin(3C+
sin(3C+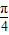 )=
)= ,
,
∴sin(3C+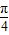 )=
)=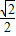 ,又0<C<
,又0<C<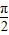 ,
,
∴3C+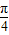 ∈(
∈(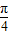 ,
,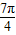 ),
),
∴3C+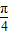 =
=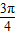 ,故C=
,故C=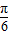 …9分
…9分
∵c2=a2+b2-2abcosC,c=1,
∴1=a2+b2-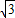 ab≥(2-
ab≥(2-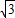 )ab,
)ab,
∴ab≤2+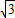 …11分
…11分
∴S△ABC= absinC=
absinC= ab≤
ab≤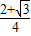 …13分
…13分
∴△ABC面积的最大值为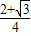 …14分
…14分
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,考查余弦定理与三角形面积,考查基本不等式的应用,属于中档题.
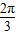 ,从而可求ω,由函数f(x)=Asin(ωx+φ)的图象经过(
,从而可求ω,由函数f(x)=Asin(ωx+φ)的图象经过(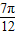 ,-
,- )及0<φ<π可求得φ,又f(
)及0<φ<π可求得φ,又f(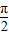 )=-
)=- 可求A;
可求A;(2)在锐角△ABC中,由f(C)=
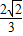 sin(3C+
sin(3C+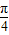 )=
)= ,可求C;利用余弦定理c2=a2+b2-2abcosC,c=1及基本不等式可求得ab≤2+
,可求C;利用余弦定理c2=a2+b2-2abcosC,c=1及基本不等式可求得ab≤2+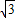 ,从而可得答案.
,从而可得答案.解答:解:(1)由题意得,
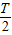 =
=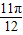 -
-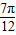 =
=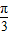 ,故T=
,故T=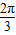 ,
,∴ω=3…2分
又当x=
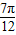 时,3x+φ=
时,3x+φ=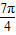 +φ=2kπ,k∈Z,
+φ=2kπ,k∈Z,∵0<φ<π,
∴φ=
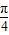 …4分
…4分 ∴f(x)=Asin(3x+
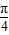 );
);又f(
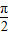 )=-
)=- ,
,∴A=
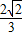 …6分
…6分∴f(x)=
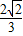 sin(3x+
sin(3x+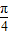 );…7分
);…7分(2)由f(C)=
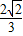 sin(3C+
sin(3C+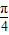 )=
)= ,
,∴sin(3C+
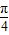 )=
)=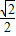 ,又0<C<
,又0<C<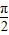 ,
,∴3C+
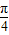 ∈(
∈(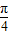 ,
,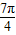 ),
),∴3C+
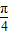 =
=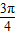 ,故C=
,故C=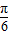 …9分
…9分∵c2=a2+b2-2abcosC,c=1,
∴1=a2+b2-
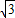 ab≥(2-
ab≥(2-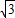 )ab,
)ab,∴ab≤2+
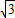 …11分
…11分∴S△ABC=
 absinC=
absinC= ab≤
ab≤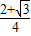 …13分
…13分∴△ABC面积的最大值为
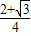 …14分
…14分点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,考查余弦定理与三角形面积,考查基本不等式的应用,属于中档题.

练习册系列答案
相关题目