题目内容
下列命题中是假命题的是( )
A、?x∈(0,
| ||
| B、?x0∈R,sinx0+cosx0=2 | ||
| C、?x∈R,3x>0 | ||
| D、?x0∈R,lgx0=0 |
分析:A利用教材结论判断正误;B根据三角函数的最值判断正误;对于C通过指数函数的性质即可判断正误;对于D找出x0的值即可判断正误;
解答:解:因为?x∈(0,
),tanx>x>sinx恒成立,所以A正确;
?x0∈R,sinx0+cosx0=
sin(x+
)≤
,所以B不正确;
由指数函数的性质可知:?x∈R,3x>0,所以C正确;
当x0=1时,说明?x0∈R,lgx0=0,所以D正确;
故选B
| π |
| 2 |
?x0∈R,sinx0+cosx0=
| 2 |
| π |
| 4 |
| 2 |
由指数函数的性质可知:?x∈R,3x>0,所以C正确;
当x0=1时,说明?x0∈R,lgx0=0,所以D正确;
故选B
点评:本题是基础题,考查三角函数的定义,三角函数线的应用,指数函数的性质,对数函数的性质,是小综合体,基本知识掌握的好坏,直接影响解题的效果.

练习册系列答案
相关题目

 ”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0垂直”的充要条件
”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0垂直”的充要条件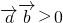 “是“
“是“ 的夹角为锐角”的充要条件
的夹角为锐角”的充要条件 ”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0垂直”的充要条件
”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0垂直”的充要条件