Question

不在同一平面的三条直线a，b，c互相平行，A、B为b上两定点，求证：另两顶点分别在a及c上的四面体体积为定值．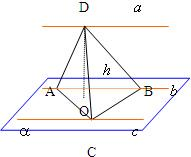

Answer 1

证明：因为A、B为直线b上两定点，而直线b∥直线c，
所以，不论点C在直线c的什么位置上，△ABC的面积均为一定值（同底等高的三角形等积），
又因直线a平行于直线b，c，
所以，直线a∥平面α（已知a，b，c不在同一平面内），
因此，不论点D在直线a的什么位置上，从点D到平面α的距离h为一定值，
故四面体ABCD的体积=

1

3

×底面积×高=

1

3

?S△ABC?h=定值．