已知f(x)=x2sinx.则函数f(x)在[-π.π]的图象是( )A．B．C．D．题目和参考答案——青夏教育精英家教网——

题目内容

1．已知f（x）=x²sinx，则函数f（x）在[-π，π]的图象是（　　）

A．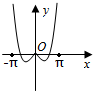

B．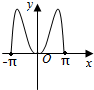

C．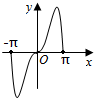

D．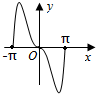

分析根据函数f（x）=x²sinx是奇函数，且函数在[0，π]上的函数值为正实数，从而得出结论．

解答解：由于函数f（x）=x²sinx是奇函数，
故它的图象关于原点对称，且当x∈[0，π]时，函数值为正实数，
故选：C．

点评本题主要考查奇函数的图象和性质，正弦函数在∈[0，π]上的值域，属于基础题．

练习册系列答案

深圳市初中学业水平考试系列答案

小升初集结号系列答案

名著导读全析精练系列答案

学科教学基本要求系列答案

寒假学习与应用系列答案

活动填图册系列答案

有效课堂精讲精练系列答案

新课程初中物理同步训练系列答案

单元测评四川教育出版社系列答案

相关题目

11．已知向量$\overrightarrow{a}$=（cos$\frac{3}{2}$x，sin$\frac{3}{2}$x），$\overrightarrow{b}$=（cos$\frac{x}{2}$，sin$\frac{x}{2}$），且x∈[0，$\frac{2π}{3}$]．
（1）求$\overrightarrow{a}$•$\overrightarrow{b}$及|$\overrightarrow{a}$+$\overrightarrow{b}$|；
（2）若f（x）=$\overrightarrow{a}$•$\overrightarrow{b}$-2λ|$\overrightarrow{a}$+$\overrightarrow{b}$|的最小值为-$\frac{3}{2}$，求实数λ的值．

12．设函数f（x）和g（x）分别是R上的偶函数和奇函数，则下列函数为偶函数的是（　　）

f（x）+g（-x）

g（x）-g（-x）

f（x）g（x）

9．若函数f（x）=sin²ax-$\sqrt{3}$sinax•cosax-$\frac{1}{2}$（a＞0）的图象与直线y=b相切，并且切点的横坐标依次成公差为$\frac{π}{2}$的等差数列．
（Ⅰ）求a，b的值；
（Ⅱ）若x₀∈[0，$\frac{π}{2}$]，且x₀是y=f（x）的零点，试写出函数y=f（x）在[x₀，x₀+$\frac{π}{2}$]上的单调增区间．

16．设m是实数，若函数f（x）=|x-m|-|x-1|是定义在R上的奇函数，则m=1或-1．

6．若函数f（x）=log${\;}_{\frac{1}{2}}$（-x²+4x+5）在区间（3m-2，m+2）内单调递增，则实数m的取值为（　　）

[$\frac{4}{3}，3$]

[$\frac{4}{3}，2$]

[$\frac{4}{3}，2$）

[$\frac{4}{3}，+∞$）

13．已知集合A={x|x²-2x-3≤0}，B={x|x＜a}，若A⊆B，则实数a的取值范围是（　　）

（-1，+∞）

10．已知实数a，b，c满足a²+b²+c²=3．
（Ⅰ）求证a+b+c≤3；
（Ⅱ）求证$\frac{1}{{a}^{2}}+\frac{1}{{b}^{2}}+\frac{1}{{c}^{2}}≥3$．

11．在区间[-2，2]上任取一个实数，则该数是不等式x²＜1的解的概率为$\frac{1}{2}$．