题目内容
已知数列{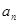 }中
}中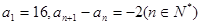 ,则数列
,则数列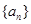 的前n项和
的前n项和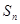 最大时,n的值为 ( )
最大时,n的值为 ( )
| A.8 | B.7或8 | C.8或9 | D.9 |
C
解析试题分析:由题意知{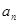 }为等差数列,且公差为-2,所以
}为等差数列,且公差为-2,所以 由
由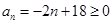 得
得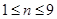 ,因为
,因为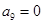 ,所以数列
,所以数列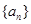 的前n项和
的前n项和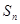 最大时,n的值为8或9.
最大时,n的值为8或9.
考点:等差数列的定义及前n项和的最值问题。
点评:根据等差数列的定义可知{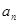 }为等差数列,从而求出其通项公式,然后利用通项公式
}为等差数列,从而求出其通项公式,然后利用通项公式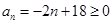 得
得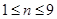 ,从而确定了前8或9项和最大,也可利用前n项公式借助二次函数的性质求最值。
,从而确定了前8或9项和最大,也可利用前n项公式借助二次函数的性质求最值。

练习册系列答案
相关题目
数列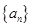 的首项为
的首项为 ,
,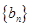 为等差数列且
为等差数列且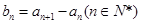 .若则
.若则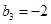 ,
,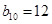 ,则
,则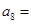 ( )
( )
| A.0 | B.3 | C.8 | D.11 |
在等差数列3,7,11 …中,第5项为
| A.15 | B.18 | C.19 | D.23 |
在首项为57,公差为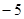 的等差数列
的等差数列 中,最接近零的是第( ) 项.
中,最接近零的是第( ) 项.
| A.14 | B.13 | C.12 | D.11 |
等差数列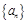 中,若
中,若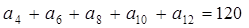 ,则
,则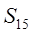 的值为:
的值为:
| A.180 | B.240 | C.360 | D.720 |
设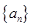 是等差数列,且
是等差数列,且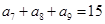 ,则其前15项和
,则其前15项和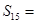 ( )
( )
| A.15 | B.45 | C.75 | D.105 |
数列 中,
中,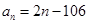 ,则使前n项和
,则使前n项和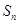 取得最小值的n的值为
取得最小值的n的值为
| A.52 | B.53 | C.54 | D.52或53 |
在等差数列{ 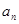 }中,
}中,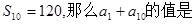 ( )
( )
| A.12 | B.24 | C.36 | D.48 |
已知数列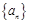 是等差数列,
是等差数列,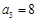 ,
,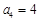 ,则前
,则前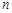 项和
项和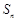 中最大的是( )
中最大的是( )
A.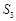 | B.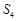 或 或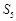 | C.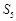 或 或 | D. |