题目内容
已知命P：a＞1，Q：（a-1）（a+1）＞0，P是Q成立的
- A.充分而不必要条件
- B.必要而不充分条件
- C.充分必要条件
- D.既不充分也不必要条件
A
分析：由（a-1）（a+1）＞0，可解得，a＜-1，或a＞1．故a＞1是a＜-1，或a＞1成立的充分不必要条件，即P是Q成立的充分不必要条件．
解答：由（a-1）（a+1）＞0，可解得，a＜-1，或a＞1
而集合{a|a＞1}是集合{a|a＜-1，或a＞1}的真子集，
故a＞1是a＜-1，或a＞1成立的充分不必要条件，
即P是Q成立的充分不必要条件．
故选A．
点评：本题为充要条件的判断，要注意必要条件、充分条件与充要条件的判断的技巧．属基础题
分析：由（a-1）（a+1）＞0，可解得，a＜-1，或a＞1．故a＞1是a＜-1，或a＞1成立的充分不必要条件，即P是Q成立的充分不必要条件．
解答：由（a-1）（a+1）＞0，可解得，a＜-1，或a＞1
而集合{a|a＞1}是集合{a|a＜-1，或a＞1}的真子集，
故a＞1是a＜-1，或a＞1成立的充分不必要条件，
即P是Q成立的充分不必要条件．
故选A．
点评：本题为充要条件的判断，要注意必要条件、充分条件与充要条件的判断的技巧．属基础题
练习册系列答案
相关题目
已知命p：?x∈R，使得x+
＜2，命题q：?x∈R，x2+x+1＞0，下列结论正确的是（ ）
| 1 |
| x |
| A、命题“p∧q”是真命题 |
| B、命题“（￢p）∧q”是真命题 |
| C、命题“p∧（￢q）”是真命题 |
| D、命题“（￢p）∧（￢q）”是真命题 |
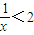，命题q：?x∈R，x2+x+1＞0，下列结论正确的是（ ）