Question

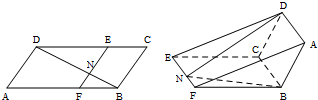
如图，已知ABCD为平行四边形，∠A=60°，AF=2FB，AB=6，点E在CD上，EF∥BC，BD⊥AD，BD交EF于点N，现将四边形ADEF沿EF折起，使点D在平面BCEF上的射影恰在直线BC上。
(Ⅰ)求证：BD⊥平面BCEF；
(Ⅱ)求折后直线DN与直线BF所成角的余弦值。

Answer 1

(Ⅰ)证明：EF⊥DN，EF⊥BN， ∴EF⊥平面BDN， ∴平面BDN⊥平面BCEF， 又因为BN为平面BDN与平面BCEF的交线， ∴D在平面BCEF上的射影在直线BN上， 而D在平面BCEF上的射影在BC上， ∴D在平面BCEF上的射影即为点B， 即BD⊥平面BCEF。
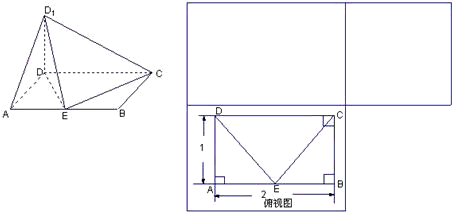
(Ⅱ)解：如图，建立空间直角坐标系，  ∵在原图中，AB=6，∠DAB=60°， 则， ∴折后图中，， ∴，， ∴，， ∴， ∴折后直线DN与直线BF所成角的余弦值为。