题目内容
设函数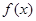 的定义域为
的定义域为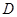 ,如果存在正实数
,如果存在正实数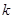 ,对于任意
,对于任意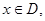 都有
都有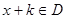 ,且
,且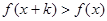 恒成立,则称函数
恒成立,则称函数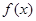 为
为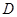 上的“
上的“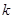 型增函数”。已知函数
型增函数”。已知函数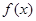 是定义在
是定义在 上的奇函数,且当
上的奇函数,且当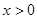 时,
时,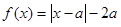 ,若
,若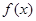 为
为 上的“
上的“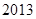 型增函数”,则实数
型增函数”,则实数 的取值范围是 .
的取值范围是 .
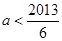
解析试题分析:  是定义在
是定义在 上的奇函数,且当
上的奇函数,且当 时,
时,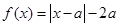 ,
,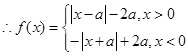
又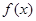 为
为 上的”
上的”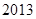 型增函数”,
型增函数”,
当 时,由定义有
时,由定义有 ,即
,即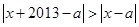 ,其几何意义为到点
,其几何意义为到点 小于到点
小于到点 的距离,由于
的距离,由于 故可知
故可知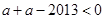 得
得 ,
,
当 时,分两类研究,若
时,分两类研究,若 ,则有
,则有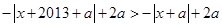 ,即
,即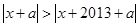 ,其几何意义表示到点
,其几何意义表示到点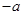 的距离小于到点
的距离小于到点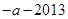 的距离,由于
的距离,由于 ,故可得
,故可得 ,得
,得 ;若
;若 ,则有
,则有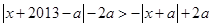 ,即
,即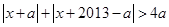 ,其几何意义表示到点
,其几何意义表示到点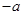 的距离与到点
的距离与到点 的距离和大于
的距离和大于 ,当
,当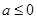 时,显然成立,当
时,显然成立,当 时,由于
时,由于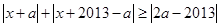 ,故有
,故有 ,必有
,必有 .解得
.解得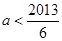 .
.
故答案: 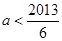
考点:本题考查奇偶性与单调性的综合.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
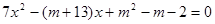
 为实数
为实数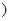 有两个实数根,且一根在
有两个实数根,且一根在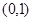 上,一根在
上,一根在 上,则
上,则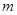 的取值范围是 .
的取值范围是 .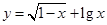 的定义域为 .
的定义域为 .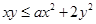 对于
对于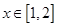 ,
,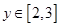 恒成立,则实数
恒成立,则实数 的取值范围是____________.
的取值范围是____________.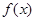 ,对
,对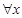 都有
都有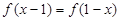 ,则
,则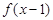 为偶函数
为偶函数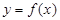 ,若对
,若对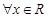 ,都有
,都有 ,则函数
,则函数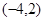 中心对称
中心对称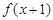 与
与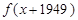 是奇函数
是奇函数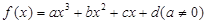 的图形一定是对称中心在图像上的中心对称图形。
的图形一定是对称中心在图像上的中心对称图形。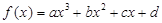 有两不同极值点
有两不同极值点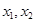 ,若
,若 ,且
,且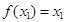 ,则关于
,则关于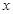 的方程
的方程 的不同实根个数必有三个.
的不同实根个数必有三个.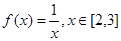 的最大值为 .
的最大值为 .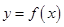 的图象与函数
的图象与函数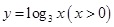 的图象关于直线
的图象关于直线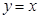 对称,则
对称,则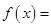 .
.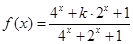 ,若对任意的实数
,若对任意的实数 ,不等式
,不等式 恒成立,则实数
恒成立,则实数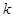 的取值范围是 .
的取值范围是 .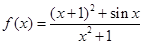 的最大值为
的最大值为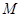 ,最小值为
,最小值为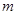 ,则
,则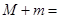 __________.
__________.