题目内容
已知直线![]() ,直线
,直线![]() 其中
其中![]()
(1)求直线![]() 的概率;
的概率;
(2)求直线与![]() 的交点位于第一象限的概率.
的交点位于第一象限的概率.
解析:(1)依题意知,直线的斜率![]() ,直线
,直线![]() 的斜率
的斜率![]() .
.
设事件![]() 为“直线
为“直线![]() ”.
”.
![]() 的基本事件为:(1,1),(1,2),…,(1,6),(2,1)(2,2),…,(2,6),…,(6,5),(6,6),共36种.
的基本事件为:(1,1),(1,2),…,(1,6),(2,1)(2,2),…,(2,6),…,(6,5),(6,6),共36种.
若![]() ,则∥
,则∥![]() ,则
,则![]() ,即
,即![]()
满足条件的实数对![]() 有(1,2)、(2,4)、(3,6),共3种.
有(1,2)、(2,4)、(3,6),共3种.
所以![]() .
.
答:直线![]() 的概率为
的概率为![]() .
.
(2)设事件![]() 为“直线与
为“直线与![]() 的交点位于第一象限”,由于直线与
的交点位于第一象限”,由于直线与![]() 有交点,则
有交点,则![]() .
.
联立方程![]() ,解得
,解得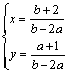
因为直线与![]() 的交点位于第一象限,则
的交点位于第一象限,则![]() ,
,
即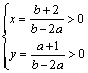 ,解得
,解得![]() .
.
![]() 的基本事件为:(1,1),(1,2),…,(1,6),(2,1)(2,2),…,(2,6),…,(6,5),(6,6),共36种.
的基本事件为:(1,1),(1,2),…,(1,6),(2,1)(2,2),…,(2,6),…,(6,5),(6,6),共36种.
满足条件的实数对![]() 有(1,3)、(1,4)、(1,5)、(1,6)、(2,5)、(2,6),共6种.
有(1,3)、(1,4)、(1,5)、(1,6)、(2,5)、(2,6),共6种.
所以![]() .
.
答:直线与![]() 的交点位于第一象限的概率为
的交点位于第一象限的概率为![]() .
.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
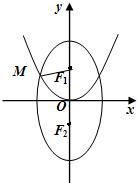 与向量、圆交汇.例5:已知F1、F2分别为椭圆C1:
与向量、圆交汇.例5:已知F1、F2分别为椭圆C1: (
( ),过点
),过点 作抛物线
作抛物线 的切线,切点分别为
的切线,切点分别为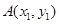 、
、 (其中
(其中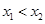 ).
). ,求
,求 与
与 的值;
的值; 与直线
与直线 相切,求圆
相切,求圆 ,且以点
,且以点 与曲线
与曲线 相切,且过点
相切,且过点 ,∴
,∴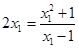 ,利用求根公式得到结论先求直线
,利用求根公式得到结论先求直线 的方程,再利用点P到直线的距离为半径,从而得到圆的方程。
的方程,再利用点P到直线的距离为半径,从而得到圆的方程。 ,借助于函数的性质圆
,借助于函数的性质圆
 可得,
可得, . ------1分
. ------1分 ,
,
 ,或
,或 , --------------------3分
, --------------------3分 ,或
,或 ----------------4分
----------------4分 ,
, ,
, ,则
,则 ,
, ,又
,又 ,
, ,即
,即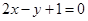 . -----------------7分
. -----------------7分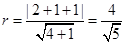 ,--------------8分
,--------------8分 . --------------------9分
. --------------------9分
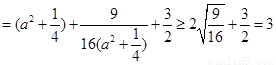 ,
, ,即
,即 ,
, 时取等号.
时取等号.