Question

【题目】为调查某市学生百米运动成绩，从该市学生中按照男女生比例随机抽取50名学生进行百米测试，测试成绩全部都介于13秒到18秒之间，将测试结果按如下方式分成五组，第一组[13,14)，第二组[14,15)，…，第五组[17,18]，如图是按上述分组方法得到的频率分布直方图.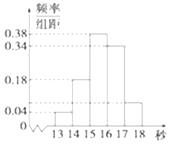

（1）设m，n表示样本中两个学生的百米测试成绩，已知m，n∈[13,14)∪[17,18]，求事件“|m－n|>2”的概率；
（2）根据有关规定，成绩小于16秒为达标.
如果男女生使用相同的达标标准，则男女生达标情况如附表：

根据上表数据，能否在犯错误的概率不超过0.01的前提下认为“体育达标与性别有关”？若有，你能否提出一个更好的解决方法来？
附：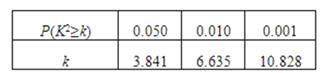

Answer 1

【答案】
（1）

解：从频率分布直方图中可以看出，成绩在 的人数为 (人)，设为 ；成绩在 的人数为 (人)，设为 .

有 一种情况； 时有 三种情况； 分别在 和 时有 六种情况，所有基本事件总数为10.

而事件“ ”由6个基本事件即 组成.

所以 .

（2）

解：依题意得到相应的 列联表如下：

.

由于 ，故在犯错误的概率不超过 的前提下认为“体育达标与性别有关”.

故可以根据男女生性别划分达标的标准.

【解析】：本题主要考查了独立性检验的应用，解决问题的关键是(1) 根据频率从分布直方图及公式 分别求出第一组和第五组的人数.然后用例举法将从这两组中随机抽取两人的所有基本事件一一例举,然后再将 的所有事件一一例举,根据古典概型概率公式求其概率. (2)根据频率分布直方图求出不达标的总人数,则可得 ,从而可得 的值.根据公式计算 ,若 说明两变量有关,否则无关.