题目内容
x的二次方程x2+z1x+z2+m=0中，z1，z2，m均是复数，且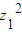
-4z2=16+20i，设这个方程的两个根α、β，满足|α-β|=2
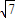，求|m|的最大值和最小值．
【答案】分析：题目给出的是复系数一元二次方程，并且给出了
，首先设出复数m，运用根与系数关系求出α+β及αβ，再借助|α-β|=2
找出复数m所满足的关系，根据几何意义求|m|的最大值和最小值．
解答：解：设m=a+bi（a，b∈R）．则z12-4z2-4m=16+20i-4a-4bi=4[（4-a）+（5-b）i]．
而|α-β|=2
?|α-β|2=28?|（α-β）2|=28?|（α+β）2-4αβ|=28
?
?|（4-a）+（5-b）i|=7?（a-4）2+（b-5）2=72，
即表示复数m的点在圆（a-4）2+（b-5）2=72上，
该点与原点距离的最大值为7+
，最小值为7-
．
点评：本题考查了复数相等的充要条件问题，考查了转化思想及数与形的结合，解答此题的关键是设出复数m，根据方程两根差的绝对值为
列式，转化为复数m的实部和虚部所满足的关系．
，首先设出复数m，运用根与系数关系求出α+β及αβ，再借助|α-β|=2找出复数m所满足的关系，根据几何意义求|m|的最大值和最小值．解答：解：设m=a+bi（a，b∈R）．则z12-4z2-4m=16+20i-4a-4bi=4[（4-a）+（5-b）i]．
而|α-β|=2
?|α-β|2=28?|（α-β）2|=28?|（α+β）2-4αβ|=28?
?|（4-a）+（5-b）i|=7?（a-4）2+（b-5）2=72，即表示复数m的点在圆（a-4）2+（b-5）2=72上，
该点与原点距离的最大值为7+
，最小值为7-．点评：本题考查了复数相等的充要条件问题，考查了转化思想及数与形的结合，解答此题的关键是设出复数m，根据方程两根差的绝对值为
列式，转化为复数m的实部和虚部所满足的关系． 
练习册系列答案
相关题目
关于x的二次方程x2-（2+i）x+1+ai=0，（a∈R）有实根，则复数z=
对应的点在（ ）
| 2-ai |
| a+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |