题目内容
设函数f(x)=x2+aln(1+x)有两个极值点x1,x2,且x1<x2,
(Ⅰ)求a的取值范围,并讨论f(x)的单调性;
(Ⅱ)证明: 。
。
(Ⅰ)求a的取值范围,并讨论f(x)的单调性;
(Ⅱ)证明:
 。
。 (Ⅰ)解:由题设知,函数f(x)的定义域是x>-1,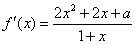 ,
,
且f′(x)=0有两个不同的根x1、x2,
故2x2+2x+a=0的判别式△=4-8a>0,即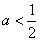 ,
,
且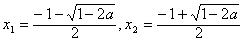 ,
,
又x1>-1,故a>0,
因此a的取值范围是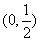 ,
,
当x变化时,f(x)与f′(x)的变化情况如下表:

因此f(x)在区间(-1,x1)和(x2,+∞)内是增函数,在区间(x1,x2)是减函数。
(Ⅱ)证明:由题设和(Ⅰ)知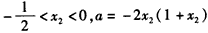 ,
,
于是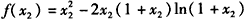 ,
,
设函数g(t)=t2-2t(1+t)ln(1+t),
则g′(t)=-2(1+2t)ln(1+t),
当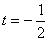 时,g′(t)=0;当
时,g′(t)=0;当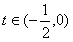 时,g′(t)>0;
时,g′(t)>0;
故g(t)在区间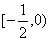 内是增函数,
内是增函数,
于是,当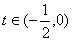 时,
时,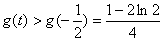 ,
,
因此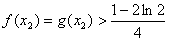 。
。
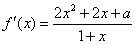 ,
,且f′(x)=0有两个不同的根x1、x2,
故2x2+2x+a=0的判别式△=4-8a>0,即
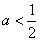 ,
,且
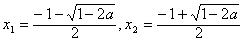 ,
,又x1>-1,故a>0,
因此a的取值范围是
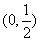 ,
,当x变化时,f(x)与f′(x)的变化情况如下表:

因此f(x)在区间(-1,x1)和(x2,+∞)内是增函数,在区间(x1,x2)是减函数。
(Ⅱ)证明:由题设和(Ⅰ)知
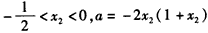 ,
,于是
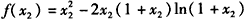 ,
,设函数g(t)=t2-2t(1+t)ln(1+t),
则g′(t)=-2(1+2t)ln(1+t),
当
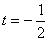 时,g′(t)=0;当
时,g′(t)=0;当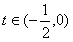 时,g′(t)>0;
时,g′(t)>0;故g(t)在区间
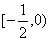 内是增函数,
内是增函数,于是,当
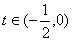 时,
时,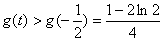 ,
,因此
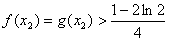 。
。 
练习册系列答案
相关题目
 设函数
设函数 设函数
设函数